
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与x轴平行,求a的值;
处的切线与x轴平行,求a的值;
(Ⅱ)若![]() 在
在![]() 处取得极大值,求a的取值范围;
处取得极大值,求a的取值范围;
(Ⅲ)当a=2时,若函数![]() 有3个零点,求m的取值范围.(只需写出结论)
有3个零点,求m的取值范围.(只需写出结论)
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(Ⅰ)对函数求导,由点![]() 处的切线与
处的切线与![]() 轴平行可得
轴平行可得![]() ,即可求出实数
,即可求出实数![]() ;
;
(Ⅱ)对函数求导可得![]() ,令导数等于零,解得
,令导数等于零,解得![]() ,
,![]() ,分类讨论
,分类讨论![]() 与
与![]() 的大小,即可求出实数
的大小,即可求出实数![]() 的范围,使得
的范围,使得![]() 在
在![]() 处取得极大值;
处取得极大值;
(Ⅲ)对![]() 求导,分别讨论
求导,分别讨论![]() 大于零和小于零时函数的单调性,结合单调性,讨论函数极值的正负,即可求出使函数
大于零和小于零时函数的单调性,结合单调性,讨论函数极值的正负,即可求出使函数![]() 有3个零点时,
有3个零点时,![]() 的取值范围。
的取值范围。
(Ⅰ)函数![]() 的定义域为
的定义域为![]() .
.![]() .
.
因为曲线![]() 在点
在点![]() 处的切线与x轴平行,
处的切线与x轴平行,
所以![]() ,解得
,解得![]() .此时
.此时![]() ,所以
,所以![]() 的值为
的值为![]() .
.
(Ⅱ)因为![]() ,
,
①若![]() ,
,
则当![]() 时,
时,![]() ,所以
,所以![]() ;
;
当![]() 时,
时,![]() ,所以
,所以![]() .
.
所以![]() 在
在![]() 处取得极大值.
处取得极大值.
②若![]() ,则当
,则当![]() 时,
时,![]() ,
,
所以![]() .所以
.所以![]() 不是
不是![]() 的极大值点.
的极大值点.
综上可知,![]() 的取值范围为
的取值范围为![]() .
.
(Ⅲ)当![]() 时,
时,![]()
![]() ,
,
![]()
![]() ,
,
当![]() 时,函数
时,函数![]() ,不可能3个零点;
,不可能3个零点;
①当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,![]()
令![]() ,得
,得![]() ,则
,则![]() 在区间
在区间![]() 上单调递增;
上单调递增;
令![]() ,解得:
,解得:![]() 或
或![]() ,则
,则![]() 在区间
在区间![]() 和
和![]() 上单调递减;
上单调递减;
由于当![]() 时,
时,![]() 恒成立,
恒成立,![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() 恒成立,所以函数
恒成立,所以函数![]() 最多只有两个零点,即
最多只有两个零点,即![]() 不满足题意;
不满足题意;
②当![]() 时,令
时,令![]() ,解得:
,解得:![]() ,
,![]()
令![]() ,得:
,得:![]() 或
或![]() ,则
,则![]() 在区间
在区间![]() 和
和![]() 上单调递增;
上单调递增;
令![]() ,解得:
,解得:![]() ,则
,则![]() 在区间
在区间![]() 上单调递减;
上单调递减;
![]() 要使函数
要使函数![]() 有3个零点,则
有3个零点,则![]() ,解得:
,解得:![]()
综上所述![]() 的取值范围为
的取值范围为![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】设P是抛物线y2=4x上的一个动点,F为抛物线的焦点,记点P到点A(-1,1)的距离与点P到直线x= - 1的距离之和的最小值为M,若B(3,2),记|PB|+|PF|的最小值为N,则M+N= ______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某购物网站对在7座城市的线下体验店的广告费指出![]() 万元和销售额
万元和销售额![]() 万元的数据统计如下表:
万元的数据统计如下表:
城市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合y与x关系,求y关于x的线性回归方程.
(2)若用对数函数回归模型拟合y与x的关系,可得回归方程![]() ,经计算对数函数回归模型的相关指数约为0.95,请说明选择哪个回归模型更合适,并用此模型预测A城市的广告费用支出8万元时的销售额.
,经计算对数函数回归模型的相关指数约为0.95,请说明选择哪个回归模型更合适,并用此模型预测A城市的广告费用支出8万元时的销售额.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式: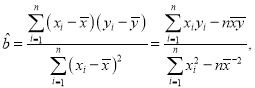
![]() ,
,
相关指数: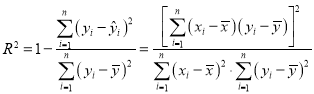 (注意:
(注意:![]() 与
与![]() 公式中的相似之处)
公式中的相似之处)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线![]() 的焦点,F关于原点的对称点为
的焦点,F关于原点的对称点为![]() ,点M在抛物线C上,给出下列三个结论:
,点M在抛物线C上,给出下列三个结论:
①使得![]() 为等腰三角形的点M有且仅有6个
为等腰三角形的点M有且仅有6个
②使得![]() 的点M有且仅有2个
的点M有且仅有2个
③使得![]() 的点M有且仅有4个
的点M有且仅有4个
其中正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
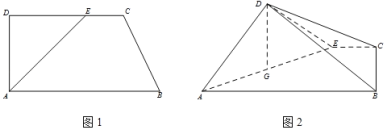
【题目】已知三棱锥![]() (如图1)的平面展开图(如图2)中,四边形
(如图1)的平面展开图(如图2)中,四边形![]() 为边长为
为边长为![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥
的正方形,△ABE和△BCF均为正三角形,在三棱锥![]() 中:
中:
(I)证明:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)若点![]() 在棱
在棱![]() 上,满足
上,满足![]() ,
, ![]() ,点
,点![]() 在棱
在棱![]() 上,且
上,且![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图),
(如图),![]() 为
为![]() 中点.
中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求四棱锥![]() 的体积;
的体积;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;
②在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
③若两个变量间的线性相关关系越强,则相关系数![]() 的值越接近于1;
的值越接近于1;
④对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大.
有关系”的把握越大.
其中正确的命题序号是( )
A.①②③B.①②C.①③④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() 是椭圆短轴的一个顶点,且
是椭圆短轴的一个顶点,且![]() 是面积为
是面积为![]() 的等腰直角三角形.
的等腰直角三角形.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知直线![]() :
:![]() 与椭圆
与椭圆![]() 交于不同的
交于不同的![]() ,
,![]() 两点,若椭圆
两点,若椭圆![]() 上存在点
上存在点![]() ,使得四边形
,使得四边形![]() 恰好为平行四边形,求直线
恰好为平行四边形,求直线![]() 与坐标轴围成的三角形面积的最小值.
与坐标轴围成的三角形面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com