
【题目】已知等差数列{an}的前n项和为Sn , 其中a2=﹣2,S6=6.
(1)求数列{an}的通项;
(2)求数列{|an|}的前n项和为Tn .
【答案】
(1)解:设等差数列{an}的首项为a1,公差为d,
由已知得:  ,
,
∴an=﹣4+(n﹣1)×2=2n﹣6
(2)解: ![]() ,
,
当n<3时,an<0,此时 ![]() ,
,
当n≥3时,an≥0,此时Tn=﹣a1﹣a2+a3+a4+…+an
= ![]() ,
,
综上: ![]()
【解析】(1)根据等差数列的通项公式和求和公式,解出a1和d,从而得到通项公式,(2)当n<3时,an<0,此时 T n = S n = 5 n n 2 ,当n≥3时,an≥0,此时Tn=﹣a1﹣a2+a3+a4+…+an,得出答案.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.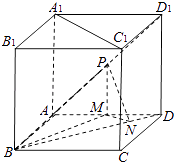
(1)求异面直线PN与A1C1所成角的大小;(结果可用反三角函数值表示)
(2)求三棱锥P﹣BMN的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设事件A表示“关于x的一元二次方程x2+ax+b2=0有实根”,其中a,b为实常数. (Ⅰ)若a为区间[0,5]上的整数值随机数,b为区间[0,2]上的整数值随机数,求事件A发生的概率;
(Ⅱ)若a为区间[0,5]上的均匀随机数,b为区间[0,2]上的均匀随机数,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,a1=2,点列Pn(n=1,2,…)在△ABC内部,且△PnAB与△PnAC的面积比为2:1,若对n∈N*都存在数列{bn}满足 ![]() ,则a4的值为 .
,则a4的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:m∈R,使 ![]() 是幂函数,且在(0,+∞)上单调递减;命题q:x∈(2,+∞),x2>2x , 则下列命题为真的是( )
是幂函数,且在(0,+∞)上单调递减;命题q:x∈(2,+∞),x2>2x , 则下列命题为真的是( )
A.p∧(q)
B.(p)∧q
C.p∧q
D.(p)∨q
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生寒假期间学习情况,学校对某班男、女学生学习时间进行调查,学习时间按整小时统计,调查结果绘成折线图如下:
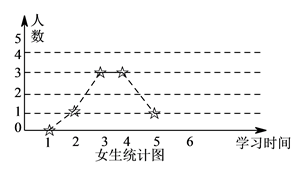
(I)已知该校有 ![]() 名学生,试估计全校学生中,每天学习不足
名学生,试估计全校学生中,每天学习不足 ![]() 小时的人数.
小时的人数.
(II)若从学习时间不少于 ![]() 小时的学生中选取
小时的学生中选取 ![]() 人,设选到的男生人数为
人,设选到的男生人数为 ![]() ,求随机变量
,求随机变量 ![]() 的分布列.
的分布列.
(III)试比较男生学习时间的方差 ![]() 与女生学习时间方差
与女生学习时间方差 ![]() 的大小.(只需写出结论).
的大小.(只需写出结论).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知(2x﹣ ![]() )5(Ⅰ)求展开式中含
)5(Ⅰ)求展开式中含 ![]() 项的系数
项的系数
(Ⅱ)设(2x﹣ ![]() )5的展开式中前三项的二项式系数之和为M,(1+ax)6的展开式中各项系数之和为N,若4M=N,求实数a的值.
)5的展开式中前三项的二项式系数之和为M,(1+ax)6的展开式中各项系数之和为N,若4M=N,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大学开设甲、乙、丙三门选修课供学生任意选修(也可不选),假设学生是否选修哪门课彼此互不影响.已知某学生只选修甲一门课的概率为0.08,选修甲和乙两门课的概率为0.12,至少选修一门的概率是0.88.
(1)求该学生选修甲、乙、丙的概率分别是多少?
(2)用ξ表示该学生选修的课程门数和没有选修的课程门数的乘积,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求f(x)的最小正周期和单调递增区间;
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对角为x,试求x的范围及此时函数f(x)的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com