
【题目】已知圆M过两点A(1,﹣1),B(﹣1,1),且圆心M在x+y﹣2=0上,
(Ⅰ)求圆M的方程;
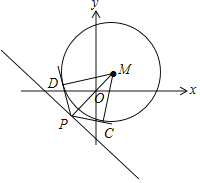
(Ⅱ)设P是直线x+y+2=0上的动点.PC,PD是圆M的两条切线,C,D为切点,求四边形PCMD面积的最小值.
【答案】(Ⅰ)(x﹣1)2+(y﹣1)2=4;(Ⅱ)最小值为4.
【解析】
(Ⅰ)根据圆心在直线AB的垂直平分线l上求解即可.
(Ⅱ)易得四边形PCMD面积为S=|PC|r,故转换为求![]() 的最小值再转换为求
的最小值再转换为求![]() 的最小值即可.
的最小值即可.
(Ⅰ)设圆心M(a,b),则a+b﹣2=0①,
又A(1,﹣1),B(﹣1,1),
∴kAB![]() ,
,
∴AB的垂直平分线l的斜率k=1,又AB的中点为O(0,0),
∴l的方程为y=x,而直线l与直线x+y﹣2=0的交点就是圆心M(a,b),
由![]() ,解得:
,解得:![]() ,又r=|MA|=2,
,又r=|MA|=2,
∴圆M的方程为(x﹣1)2+(y﹣1)2=4;
(Ⅱ)由切线的性质知:四边形PCMD的面积S=|PC|r,
四边形PCMD的面积取最小值时,|PM|最小为圆心M到直线x+y+2=0的距离,
即![]() ,得|PC|min=2.
,得|PC|min=2.
∴四边形PCMD面积的最小值为4.


科目:高中数学 来源: 题型:
【题目】已知命题p:“方程:![]() 表示焦点在x轴上的双曲线”;命题q:“关于x的不等式x2+2ax+1≥0在R上恒成立”.
表示焦点在x轴上的双曲线”;命题q:“关于x的不等式x2+2ax+1≥0在R上恒成立”.
(1)若命题p为真命题,求实数a的取值范围;
(2)若命题“p或q”为真命题,“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 分别是
分别是![]() 上的点,且
上的点,且![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是
是![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使平面
,使平面![]() 与平面
与平面![]() 垂直?说明理由.
垂直?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过焦点F的直线l与抛物线分别交于A、B两点,O为坐标原点,且
,过焦点F的直线l与抛物线分别交于A、B两点,O为坐标原点,且![]() .
.
(1)求抛物线的标准方程;
(2)对于抛物线上任一点Q,点P(2t,0)都满足|PQ|≥2|t|,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的离心率
)的离心率![]() ,直线
,直线![]() 被以椭圆
被以椭圆![]() 的短轴为直径的圆截得的弦长为
的短轴为直径的圆截得的弦长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交椭圆于
交椭圆于![]() ,
, ![]() 两个不同的点,且
两个不同的点,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1,y1),D(x2,y2)其中(x1<x2)是曲线y2=9x(y≥0).上的两点,A,D两点在x轴上的射影分别为点B,C且|BC|=3.
(Ⅰ)当点B的坐标为(1,0)时,求直线AD的方程:
(Ⅱ)记△AOD的面积为S1,梯形ABCD的面积为S2,求![]() 的范围
的范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一列非零向量![]() 满足:
满足:![]() ,
,![]() ,其中
,其中![]() 是正数
是正数
(1)求数列![]() 的通项公式;
的通项公式;
(2)求证:当![]() 时,向量
时,向量![]() 与
与![]() 的夹角为定值;
的夹角为定值;
(3)当![]() 时,把
时,把![]() 中所有与
中所有与![]() 共线的向量按原来的顺序排成一列,记为
共线的向量按原来的顺序排成一列,记为![]() ,令
,令![]() ,
,![]() 为坐标原点,求点列
为坐标原点,求点列![]() 的极限点
的极限点![]() 的坐标.(注:若点坐标为
的坐标.(注:若点坐标为![]() ,且
,且![]() ,则称点
,则称点![]() 为点列的极限点)
为点列的极限点)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中药种植基地有两处种植区的药材需在下周一、下周二两天内采摘完毕,基地员工一天可以完成一处种植区的采摘.由于下雨会影响药材品质,基地收益如下表所示:
周一 | 无雨 | 无雨 | 有雨 | 有雨 |
周二 | 无雨 | 有雨 | 无雨 | 有雨 |
收益 |
|
|
|
|
若基地额外聘请工人,可在周一当天完成全部采摘任务.无雨时收益为![]() 万元;有雨时,收益为
万元;有雨时,收益为![]() 万元.额外聘请工人的成本为
万元.额外聘请工人的成本为![]() 万元.
万元.
已知下周一和下周二有雨的概率相同,两天是否下雨互不影响,基地收益为![]() 万元的概率为
万元的概率为![]() .
.
(Ⅰ)若不额外聘请工人,写出基地收益![]() 的分布列及基地的预期收益;
的分布列及基地的预期收益;
(Ⅱ)该基地是否应该外聘工人,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了110人,其中女性50人,男性60人.女性中有30人主要的休闲方式是看电视,另外20人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外40人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 列联表;
列联表;
(2)判断是否有99%的把握认为性别与休闲方式有关系.
下面临界值表供参考:
| 0.10 | 0.05 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
(参考公式: )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com