
【题目】设函数![]() ,
,
(1)求函数f(x)在x∈[﹣1,2]上的最大值和最小值;
(2)若对于任意x∈[﹣1,2]都有f(x)<m成立,求实数m的取值范围.
【答案】(1)最大值为7,最小值为![]() ;(2)
;(2)![]()
【解析】
(1)函数求导得![]() =3x2﹣x﹣2=(3x+2)(x﹣1),(x∈R),易知在区间(﹣1,
=3x2﹣x﹣2=(3x+2)(x﹣1),(x∈R),易知在区间(﹣1,![]() ),(1,2)上,
),(1,2)上,![]() >0,在区间(
>0,在区间(![]() ,1)上,
,1)上,![]() <0,从而求得函数的极值,再计算给定区间的端点函数值,其中最大的为最大值;最小的为最小值.
<0,从而求得函数的极值,再计算给定区间的端点函数值,其中最大的为最大值;最小的为最小值.
(2)对于任意x∈[﹣1,2]都有f(x)<m成立,只需要f(x)max<m即可.
(1)f′(x)=3x2﹣x﹣2=(3x+2)(x﹣1),(x∈R),
因为在区间(﹣1,![]() ),(1,2)上,
),(1,2)上,![]() >0,
>0,
所以f(x)单调递增,
因为在区间(![]() ,1)上,
,1)上,![]() <0,
<0,
所以f(x)单调递减,
所以f(x)极大值=f(![]() )
)![]() ,f(x)极小值=f(1)
,f(x)极小值=f(1)![]() ,
,
又因为f(﹣1)![]() ,f(2)=7,
,f(2)=7,
所以f(x)在x∈[﹣1,2]上的最大值为7,最小值为![]() .
.
(2)若对于任意x∈[﹣1,2]都有f(x)<m成立,
则只需要f(x)max<m即可,
由(1)知,f(x)在x∈[﹣1,2]上的最大值为7,
所以m>7.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,△DAB≌△DCB,E为线段BD上的点,且EA=EB=ED=AB,延长CE交AD于点F.
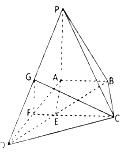
(1)若G为PD的中点,求证平面PAD⊥平面CGF;
(2)若AD=AP=6,求平面BCP与平面DCP所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆E:![]() y2=1的左、右焦点,过点P(﹣2,0)的直线l与椭圆E有且只有一个交点T.
y2=1的左、右焦点,过点P(﹣2,0)的直线l与椭圆E有且只有一个交点T.
(1)求△F1TF2的面积;
(2)求证:光线![]() 被直线反射后经过F2.
被直线反射后经过F2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式|x﹣1|+|2x+1|<3的解集为{x|a<x<b};
(1)求a,b的值;
(2)若正实数x,y满足x+y=ab+2且不等式(yc2﹣4)x+(8cx﹣1)y≤0对任意的x,y恒成立,求实数c的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线
,在以坐标原点为极点,x轴非负半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() Ⅰ
Ⅰ![]() 写出
写出![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
![]() Ⅱ
Ⅱ![]() 若
若![]() 与
与![]() 相交于A,B两点,求
相交于A,B两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,且
,且![]() .点
.点![]() 是线段
是线段![]() 上一点,且
上一点,且![]() .
.
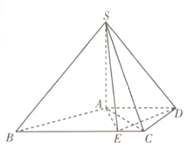
(1)求证:平面![]() 平面
平面![]() .
.
(2)若![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 到平面
到平面![]() 的距离为
的距离为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是由
是由![]() 个有序实数构成的一个数组,记作:
个有序实数构成的一个数组,记作:![]() .其中
.其中![]() 称为数组
称为数组![]() 的“元”,
的“元”,![]() 称为
称为![]() 的下标,如果数组
的下标,如果数组![]() 中的每个“元”都是来自数组
中的每个“元”都是来自数组![]() 中不同下标的“元”,则称
中不同下标的“元”,则称![]() 为
为![]() 的子数组.定义两个数组
的子数组.定义两个数组![]() ,
,![]() 的关系数为
的关系数为![]() .
.
(1)若![]() ,
,![]() ,设
,设![]() 是
是![]() 的含有两个“元”的子数组,求
的含有两个“元”的子数组,求![]() 的最大值;
的最大值;
(2)若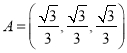 ,
,![]() ,且
,且![]() ,
,![]() 为
为![]() 的含有三个“元”的子数组,求
的含有三个“元”的子数组,求![]() 的最大值;
的最大值;
(3)若数组![]() 中的“元”满足
中的“元”满足![]() ,设数组
,设数组![]() 含有四个“元”
含有四个“元”![]() ,且
,且![]() ,求
,求![]() 与
与![]() 的所有含有三个“元”的子数组的关系数
的所有含有三个“元”的子数组的关系数![]() (
(![]() )的最大值.
)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com