
【题目】已知双曲线![]() 的右焦点到渐近线的距离为3.现有如下条件:①双曲线
的右焦点到渐近线的距离为3.现有如下条件:①双曲线![]() 的离心率为
的离心率为![]() ; ②双曲线
; ②双曲线![]() 与椭圆
与椭圆![]() 共焦点; ③双曲线右支上的一点
共焦点; ③双曲线右支上的一点![]() 到
到![]() 的距离之差是虚轴长的
的距离之差是虚轴长的![]() 倍.
倍.
请从上述3个条件中任选一个,得到双曲线![]() 的方程为_____________.
的方程为_____________.
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】某厂销售部以箱为单位销售某种零件,每箱的定价为200元,低于100箱按原价销售;不低于100箱通过双方议价,买方能以优惠![]() 成交的概率为0.6,以优惠
成交的概率为0.6,以优惠![]() 成交的概率为0.4.
成交的概率为0.4.
(1)甲、乙两单位都要在该厂购买150箱这种零件,两单位各自达成的成交价相互独立,求甲单位优惠比例不低于乙单位优惠比例的概率;
(2)某单位需要这种零件650箱,求购买总价![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ABCD所在平面垂直于直角梯形ABPE所在平面,EP![]() ,BP=2,AD=AE=1,AE⊥EP,AE∥BP,G,F分别是BP,BC的中点.
,BP=2,AD=AE=1,AE⊥EP,AE∥BP,G,F分别是BP,BC的中点.
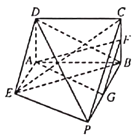
(1)求证:平面AFG∥平面PCE;
(2)求四棱锥D﹣ABPE的体积与三棱锥P﹣BCD的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,2Sn+2n=an+1﹣2,a2=8,其中n∈N*.
(1)记bn=an+1,求证:{bn}是等比数列;
(2)设![]() 为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
为数列{cn}的前n项和,若不等式k>Tn对任意的n∈N*恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】杨辉,字谦光,南宋时期杭州人.在他1261年所著的《详解九章算法》一书中,辑录了如图所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪中叶(约公元1050年)贾宪的《释锁算术》,并绘画了“古法七乘方图”.故此,杨辉三角又被称为“贾宪三角”.杨辉三角是一个由数字排列成的三角形数表,一般形式如下:
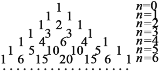
基于上述规律,可以推测,当![]() 时,从左往右第22个数为_____________.
时,从左往右第22个数为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .直线
.直线![]() 与
与![]() 轴正半轴和
轴正半轴和![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,与椭圆分别交于点
,与椭圆分别交于点![]() 、
、![]() ,各点均不重合且满足
,各点均不重合且满足![]() ,
,![]() .
.
(1)求椭圆的标准方程;
(2)若![]() ,试证明:直线
,试证明:直线![]() 过定点并求此定点.
过定点并求此定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某健身馆在2019年7、8两月推出优惠项目吸引了一批客户.为预估2020年7、8两月客户投入的健身消费金额,健身馆随机抽样统计了2019年7、8两月100名客户的消费金额,分组如下:![]() (单位:元),得到如图所示的频率分布直方图:
(单位:元),得到如图所示的频率分布直方图:
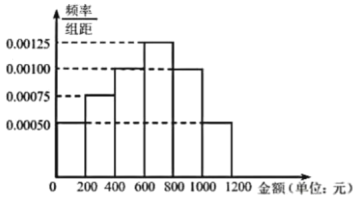
(1)若把2019年7、8两月健身消费金额不低于800元的客户,称为“健身达人”,经数据 处理,现在列联表中得到一定的相关数据,请补全空格处的数据,并根据列联表判断是否有![]() 的把握认为“健身达人”与性别有关?
的把握认为“健身达人”与性别有关?
健身达人 | 非健身达人 | 总计 | |
男 | 10 | ||
女 | 30 | ||
总计 |
(2)为吸引顾客,在健身项目之外,该健身馆特别推出健身配套营养品的销售,现有两种促销方案.
方案一:每满800元可立减100元;
方案二:金额超过800元可抽奖三次,每次中奖的概率为![]() ,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
,且每次抽奖互不影响,中奖1次打9折,中奖2次打8折,中奖3次打7折.
若某人打算购买1000元的营养品,请从实际付款金额的数学期望的角度分析应该选择哪种优惠方案.
(3)在(2)中的方案二中,金额超过800元可抽奖三次,假设三次中奖结果互不影响,且三次中奖的概率为![]() ,记
,记![]() 为锐角
为锐角![]() 的内角,
的内角,
求证:![]()
附:
|
|
|
|
|
|
|
|
|
|
|
|
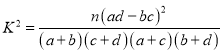
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,直线
的焦点为F,直线![]() 与抛物线C相切于点P,过点P作抛物线C的割线PQ,割线PQ与抛物线C的另一交点为Q,A为PQ的中点.过A作y轴的垂线与y轴交于点H,与直线l相交于点N,M为线段AN的中点.
与抛物线C相切于点P,过点P作抛物线C的割线PQ,割线PQ与抛物线C的另一交点为Q,A为PQ的中点.过A作y轴的垂线与y轴交于点H,与直线l相交于点N,M为线段AN的中点.
(1)求抛物线C的方程;
(2)在x轴上是否存在一点T,使得当割线PQ变化时,总有![]() 为定值?若存在,求出该点的坐标;若不存在,请说明理由.
为定值?若存在,求出该点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com