练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某迷宫有三个通道，进入迷宫的每个人都要经过一扇智能门。首次到达此门，系统会随机（即等可能）为你打开一个通道.若是1号通道，则需要1小时走出迷宫；若是2号、3号通道，则分别需要2小时、3小时返回智能门.再次到达智能门时，系统会随机打开一个你未到过的通道，直至走出迷宫为止.
    (1)求走出迷宫时恰好用了1小时的概率；
    (2)求走出迷宫的时间超过3小时的概率.
    ，
    考查数学知识的实际背景，重点考查相互独立事件的概率乘法公式计算事件的概率、随机事件的数学特征和对思维能力、运算能力、实践能力的考查。
    解：(1)设A表示走出迷宫时恰好用了1小时这一事件，则.
    (2) 设B表示走出迷宫的时间超过3小时这一事件，则.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分14分）
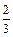    某项考试按科目A、科目B依次进行，只有当科目A成绩合格时，才可以继续参加科目B的考试。每个科目只允许有一次补考机会，两个科目成绩均合格方可获得该项合格证书，现在某同学将要参加这项考试，已知他每次考科目A成绩合格的概率均为，每次考科目B成绩合格的概率均为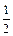。假设他在这项考试中不放弃所有的考试机会，且每次的考试成绩互不影响，记他参加考试的次数为．
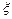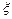    （Ⅰ）求的分布列和期望；
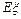    （Ⅱ）求该同学在这项考试中获得合格证书的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某射手每次射击击中目标的概率是，且各次射击的结果互不影响。
    （Ⅰ）假设这名射手射击5次，求恰有2次击中目标的概率
    （Ⅱ）假设这名射手射击5次，求有3次连续击中目标。另外2次未击中目标的概率；
    （Ⅲ）假设这名射手射击3次，每次射击，击中目标得1分，未击中目标得0分，在3次射击中，若有2次连续击中，而另外1次未击中，则额外加1分；若3次全击中，则额外加3分，记为射手射击3次后的总的分数，求的分布列。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （10分）某厂生产甲、乙两种产品，生产甲产品一等品80%，二等品20%；生产乙产品，一等品90%，二等品10%。生产一件甲产品，如果是一等品可获利4万元，若是二等品则要亏损1万元；生产一件乙产品，如果是一等品可获利6万元，若是二等品则要亏损2万元。设生产各种产品相互独立
    （1）记x（单位：万元）为生产1件甲产品和件乙产品可获得的总利润，求x的分布列
    （2）求生产4件甲产品所获得的利润不少于10万元的概率

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

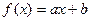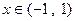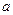    （本小题满分14分）已知函数，，、是常数．
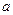    ⑴若是从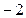、、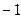、、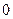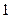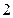五个数中任取的一个数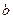，是从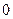、、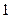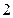三个数中任取的一个数，求函数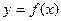为奇函数的概率．
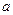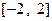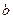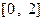    ⑵若是从区间中任取的一个数，是从区间中任取的一个数，求函数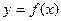有零点的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分） 
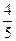    已知在3支不同编号的枪中有2支已经试射校正过，1支未经试射校正。某射手若使用其中校正过的枪，每射击一次击中目标的概率为；若使用其中未校正的枪，每射击一次击中目标的概率为，假定每次射击是否击中目标相互之间没有影响。
    （I）若该射手用这2支已经试射校正过的枪各射击一次，求目标被击中的次数为偶数的概率；
    （II）若该射手用这3支抢各射击一次，求目标至多被击中一次的概率。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某人射击1次击中目标的概率为0.6,经过3次射击，此人至少两次击中目标的概率为（  ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知（   ）
    A．—2B．2C．—12D．12

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    为了调查胃病是否与生活规律有关，对某地70名40岁以上的人进行调查，结果如下：则有多大的把握认为患胃病与生活规律有关系
    A．99.9℅B．99℅

    患胃病
    未患胃病
    合计
    生活无规律
    5
    15
    20
    生活有规律
    40
    10
    50
    合计
    45
    25
    70
    C．没有充分的证据显示有关D．1℅

    查看答案和解析>>

    同步练习册答案