
【题目】已知数列{an}满足条件:a1=1,a2=r(r>0),且{anan+1}是公比为q(q>0)的等比数列,设bn=a2n﹣1+a2n(n=1,2,…).
(1)求出使不等式anan+1+an+1an+2>an+2an+3(n∈N*)成立的q的取值范围;
(2)求bn和 ![]() ,其中Sn=b1+b2+…+bn;
,其中Sn=b1+b2+…+bn;
(3)设r=219.2﹣1,q= ![]() ,求数列{
,求数列{ ![]() }的最大项和最小项的值.
}的最大项和最小项的值.
【答案】
(1)解:由题意得rqn﹣1+rqn>rqn+1
由题设r>0,q>0,故从上式可得 q2﹣q﹣1<0,
∵q>0,故 ![]()
(2)解:∵b1=1+r≠0,所以{bn}是首项为1+r,公比为q的等比数列,从而bn=(1+r)qn﹣1
当q=1时,Sn=n(1+r), ![]() =0;
=0;
当0<q<1时 ![]() =
= ![]()
当q>1时, ![]() =0;
=0;
∴ 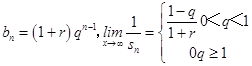
(3)解:从上式可知,设f(n)= ![]()
当n>21时,f(n)递减,∴f(n)≤f(21),∴f(n)max=2 25;
当n≤20时,f(n)递减,∴f(n)≥f(20),f(n)min=﹣4
∴当n=21时,数列{ ![]() }有最大值2 25;当n=20时,数列{
}有最大值2 25;当n=20时,数列{ ![]() }有最小值﹣4.
}有最小值﹣4.
【解析】(1)利用数列{an}满足条件:a1=1,a2=r(r>0),且{anan+1}是公比为q(q>0)的等比数列,可得公比的不等式,故可求q的取值范围;(2)先考虑相邻项的关系,可知比值为常数,故可知数列是等比数列,由于公比不定,故要进行分类讨论;(3)先求数列{ ![]() }的通项,再利用单调性,研究其最值.
}的通项,再利用单调性,研究其最值.


科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和是Sn , 则下列四个命题中,错误的是( )
A.若数列{an}是公差为d的等差数列,则数列{ ![]() }的公差为
}的公差为 ![]() 的等差数列
的等差数列
B.若数列{ ![]() }是公差为d的等差数列,则数列{an}是公差为2d的等差数列
}是公差为d的等差数列,则数列{an}是公差为2d的等差数列
C.若数列{an}是等差数列,则数列的奇数项,偶数项分别构成等差数列
D.若数列{an}的奇数项,偶数项分别构成公差相等的等差数列,则{an}是等差数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是世界读书日,为提高学生对读书的重视,让更多的人畅游于书海中,从而收获更多的知识,某高中的校学生会开展了主题为“让阅读成为习惯,让思考伴随人生”的实践活动,校学生会实践部的同学随即抽查了学校的40名高一学生,通过调查它们是喜爱读纸质书还是喜爱读电子书,来了解在校高一学生的读书习惯,得到如表列联表:
喜欢读纸质书 | 不喜欢读纸质书 | 合计 | |
男 | 16 | 4 | 20 |
女 | 8 | 12 | 20 |
合计 | 24 | 16 | 40 |
(Ⅰ)根据如表,能否有99%的把握认为是否喜欢读纸质书籍与性别有关系?
(Ⅱ)从被抽查的16名不喜欢读纸质书籍的学生中随机抽取2名学生,求抽到男生人数ξ的分布列及其数学期望E(ξ).
参考公式:K2= ![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.
下列的临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,动点P在其表面上运动,且|PA|=x,把点的轨迹长度L=f(x)称为“喇叭花”函数,给出下列结论: ① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]()
其中正确的结论是: . (填上你认为所有正确的结论序号)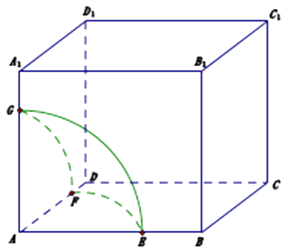
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若向量 ![]() ,在函数
,在函数 ![]() 的图象中,对称中心到对称轴的最小距离为
的图象中,对称中心到对称轴的最小距离为 ![]() ,且当
,且当 ![]() 的最大值为1.
的最大值为1.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为(参考数据: ![]() ≈1.732,sin15°≈0.2588,sin75°≈0.1305)( )
≈1.732,sin15°≈0.2588,sin75°≈0.1305)( ) 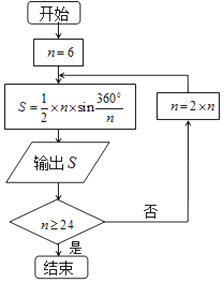
A.2.598,3,3.1048
B.2.598,3,3.1056
C.2.578,3,3.1069
D.2.588,3,3.1108
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为 ![]() ;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°
;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120° 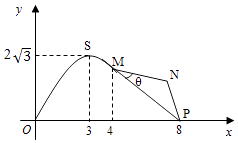
(1)求A,ω的值和M,P两点间的距离;
(2)应如何设计,才能使折线段赛道MNP最长?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的右焦点与抛物线y2=4x的焦点F重合,且椭圆的离心率是
的右焦点与抛物线y2=4x的焦点F重合,且椭圆的离心率是 ![]() ,如图所示.
,如图所示.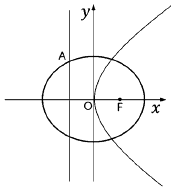
(1)求椭圆的标准方程;
(2)抛物线的准线与椭圆在第二象限相交于点A,过点A作抛物线的切线l,l与椭圆的另一个交点为B,求线段AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com