
【题目】下表数据是水的温度x(℃)对黄酮延长性y(%)效应的试验结果,y是以延长度计算的.
x/℃ | 300 | 400 | 500 | 600 | 700 | 800 |
y/% | 40 | 50 | 55 | 60 | 67 | 70 |
(1)画出散点图;
(2)指出x,y是否线性相关,若线性相关,求y关于x的回归方程;
(3)估计水的温度是1000 ℃时,黄酮延长性的情况.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】网上购物系统是一种具有交互功能的商业信息系统,它在网络上建立一个虚拟的购物商场,使购物过程变得轻松、快捷、方便.网上购物系统分为前台管理和后台管理,前台管理包括浏览商品、查询商品、订购商品、用户注册等功能;后台管理包括公告管理、商品管理、订单管理、投诉管理和用户管理等模块.根据这些要求画出该系统的结构图.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是直角△ABC斜边BC上一点,AC= ![]() DC.
DC.
(I)若∠DAC=30°,求角B的大小;
(Ⅱ)若BD=2DC,且AD=2 ![]() ,求DC的长.
,求DC的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市化工厂三个车间共有工人1 000名,各车间男、女工人数如下表:
第一车间 | 第二车间 | 第三车间 | |
女工 | 173 | 100 | y |
男工 | 177 | x | z |
已知在全厂工人中随机抽取1名,抽到第二车间男工的可能性是0. 15.
(1)求x的值;
(2)现用分层抽样的方法在全厂抽取50名工人,问应在第三车间抽取多少名?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,x轴正半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.已知曲线C的极坐标方程为ρ=2cosθ,直线l的参数方程为 ![]() (t为参数,α为直线的倾斜角).
(t为参数,α为直线的倾斜角).
(I)写出直线l的普通方程和曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C有唯一的公共点,求角α的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A、B两个投资项目的利润率分别为随机变量X1和X2,根据市场分析,X1和X2的分布列分别为
X1 | 5% | 10% |
P | 0.8 | 0.2 |
X2 | 2% | 8% | 12% |
P | 0.2 | 0.5 | 0.3 |
(1)在A,B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差V(Y1)、V(Y2);
(2)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和.求f(x)的最小值,并指出x为何值时,f(x)取到最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司生产一种品牌服装的年固定成本为10万元,且每生产1万件,需要另投入1.9万元.设R(x)(单位:万元)为销售收入,根据市场调查知R(x)= 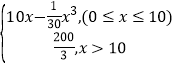 其中x(单位:万件)是年产量.
其中x(单位:万件)是年产量.
(1)写出年利润W(单位:万元)关于年产量x的函数解析式.
(2)当年产量为多少时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列语句中是命题的有________,其中是真命题的有_____(填序号).
①“垂直于同一条直线的两个平面必平行吗?”②“一个数不是正数就是负数”;③“在一个三角形中,大角所对的边大于小角所对的边”;④“若x+y为有理数,则x,y都是有理数”;⑤作一个三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com