
【题目】已知函数y=f(x)是定义在R上的偶函数,对于x∈R,都有f(x+4)=f(x)+f(2)成立,当x1 , x2∈[0,2]且x1≠x2时,都有 ![]() <0,给出下列四个命题:
<0,给出下列四个命题:
①f(﹣2)=0;
②直线x=﹣4是函数y=f(x)的图象的一条对称轴;
③函数y=f(x)在[4,6]上为增函数;
④函数y=f(x)在(﹣8,6]上有四个零点.
其中所有正确命题的序号为 .
【答案】①②④
【解析】解:①:对于任意x∈R,都有f(x+4)=f (x)+f (2)成立,令x=﹣2,则f(﹣2+4)=f(﹣2)+f (2)=f(2),
即f(﹣2)=0,即①正确;
②:由(1)知f(x+4)=f (x),则f(x)的周期为4,
又∵f(x)是R上的偶函数,∴f(x+4)=f(﹣x),
而f(x)的周期为4,则f(x+4)=f(﹣4+x),f(﹣x)=f(﹣x﹣4),
∴f(﹣4﹣x)=f(﹣4+x),
则直线x=﹣4是函数y=f(x)的图象的一条对称轴,即②正确;
③:当x1 , x2∈[0,2],且x1≠x2时,都有 ![]() <0,
<0,
∴函数y=f(x)在[0,2]上为减函数,
而f(x)的周期为4,
∴函数y=f(x)在[4,6]上为减函数,故③错误;
④:∵f(2)=0,f(x)的周期为4,函数y=f(x)在[0,2]上为增函数,
在[﹣2,0]上为减函数,
∴作出函数在(﹣8,6]上的图象如图:
则函数y=f(x)在(﹣8,6]上有4个零点,故④正确.
所以答案是.①②④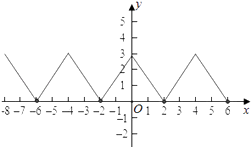
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)=a+ ![]() (a,b∈R)有最大值和最小值,且最大值与最小值之和为6,则3a﹣2b=( )
(a,b∈R)有最大值和最小值,且最大值与最小值之和为6,则3a﹣2b=( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ax2-ln x,a∈R.
ax2-ln x,a∈R.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程.
(2)讨论f(x)的单调性.
(3)是否存在a,使得方程f(x)=2有两个不等的实数根?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列题目的证法,再解决后面的问题.
已知a1,a2∈R,且a1+a2=1,求证:a+a≥![]() .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,则f(x)=2x2-2(a1+a2)x+a+a=2x2-2x+a+a.
因为对一切x∈R,恒有f(x)≥0,
所以Δ=4-8(a+a)≤0,从而得a+a≥![]() .
.
(1)若a1,a2,…,an∈R,a1+a2+…+an=1,请由上述结论写出关于a1,a2,…,an的推广式;
(2)参考上述证法,请对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=-x3+x2+b,g(x)=aln x.
(1)若f(x)在![]() 上的最大值为
上的最大值为![]() ,求实数b的值;
,求实数b的值;
(2)若对任意x∈[1,e],都有g(x)≥-x2+(a+2)x恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
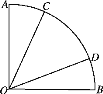
【题目】如图所示,在圆心角为90°的扇形AOB中,以圆心O作为起点作射线OC,OD,则使∠AOC+∠BOD<45°的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x﹣1)的图象关于点(1,0)对称,且当x∈(﹣∞,0),f(x)+xf′(x)<0成立.若a=(20.2)f(20.2),b=(ln2)f(ln2),c=(log2 ![]() )f(log2
)f(log2 ![]() ),则a,b,c的大小关系是( )
),则a,b,c的大小关系是( )
A.a>b>c
B.b>a>c
C.c>a>b
D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
是否需要志愿 性别 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
 附:
附:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com