
【题目】已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|﹣2≤x≤1}. (Ⅰ)求a的值;
(Ⅱ)若f(x)﹣2f( ![]() )≤k恒成立,求k的取值范围.
)≤k恒成立,求k的取值范围.
【答案】解:(Ⅰ)不等式f(x)≤3,即|ax+1|≤3,即﹣3≤ax+1≤3,即﹣4≤ax≤2. 当a>0时,求得﹣ ![]() ≤x≤
≤x≤ ![]() ,再根据它的解集为{x|﹣2≤x≤1},可得
,再根据它的解集为{x|﹣2≤x≤1},可得 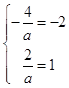 ,求得a=2.
,求得a=2.
当a<0时,求得 ![]() ≤x≤﹣
≤x≤﹣ ![]() ,再根据它的解集为{x|﹣2≤x≤1},可得
,再根据它的解集为{x|﹣2≤x≤1},可得 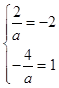 ,a无解.
,a无解.
综上可得,a=2,f(x)=|2x+1|.
(Ⅱ)若f(x)﹣2f( ![]() )≤k恒成立,即|2x+1|﹣2|x+1|≤k恒成立.
)≤k恒成立,即|2x+1|﹣2|x+1|≤k恒成立.
令g(x)=|2x+1|﹣2|x+1|= 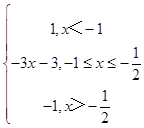 ,故函数g(x)的最大值为1,
,故函数g(x)的最大值为1,
故k≥1
【解析】(Ⅰ)由条件分类讨论,解绝对值不等式,求得不等式f(x)≤3的解集.再根据不等式f(x)≤3的解集为{x|﹣2≤x≤1},求得a的值.(Ⅱ)由题意可得|2x+1|﹣2|x+1|≤k恒成立,令g(x)=|2x+1|﹣2|x+1|,利用分段函数求得g(x)的最大值,可得k的范围.
【考点精析】掌握绝对值不等式的解法是解答本题的根本,需要知道含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:
【题目】某家具厂有方木料![]() ,五合板
,五合板![]() ,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料
,准备加工成书桌和书橱出售.已知生产每张书桌需要方木料![]() ,五合板
,五合板![]() ,生产每个书橱需要方木料
,生产每个书橱需要方木料![]() ,五合板
,五合板![]() ,出售一张书桌可获利润
,出售一张书桌可获利润![]() 元,出售一个书橱可获利润
元,出售一个书橱可获利润![]() 元.
元.
(1)如果只安排生产书桌,可获利润多少?
(2)如果只安排生产书橱,可获利润多少?
(3)怎样安排生产可使所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图已知椭圆C: ![]() +y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N.
+y2=1,以椭圆的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0).设圆T与椭圆C交于点M与点N. 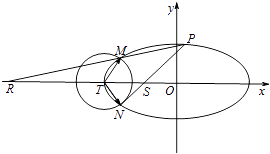
(1)求 ![]() 的最小值;
的最小值;
(2)设点P是椭圆C上异于M,N的任意一点,且直线MP,NP分别与x轴交于点R,S,O为坐标原点,求证:丨OR丨丨OS丨为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学初一年级500名学生参加某次数学测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:

(1)从总体的500名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1.设命题p:函数y=loga(x+1)在(0,+∞)内单调递减;命题q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.若p或q为真,p且q为假,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出由下列各组命题构成的“p或q”“p且q”以及“非p”形式的命题,并判断它们的真假:
(1)p:3是素数,q:3是偶数;
(2)p:x=-2是方程x2+x-2=0的解,q:x=1是方程x2+x-2=0的解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() 的图象经过点A(1,1),B(2,﹣1).
的图象经过点A(1,1),B(2,﹣1).
(1)求函数f(x)的解析式;
(2)判断函数f(x)在(0,+∞)上的单调性并用定义证明;
(3)求f(x)在区间[ ![]() ,1]上的值域.
,1]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】解答
(1)已知全集U={x|﹣5≤x≤10,x∈Z},集合M={x|0≤x≤7,x∈Z},N={x|﹣2≤x<4,x∈Z},求(UN)∩M(分别用描述法和列举法表示结果)
(2)已知全集U=A∪B={0,1,2,3,4,5,6,7,8,9,10},若集合A∩UB={2,4,6,8},求集合B;
(3)已知集合P={x|ax2+2ax+1=0,a∈R,x∈R},当集合P只有一个元素时,求实数a的值,并求出这个元素.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com