
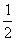 假设该产销平衡,
假设该产销平衡,(1)要不产生亏损,产量数x应控制在什么范围?
(2)生产多少台时可使利润最大?
(3)求使利润最大时产品的售价.
解:(1)生产x百台的成本为2+x万元.
当0≤x≤4时,利润为
4x-![]() x2-
x2-![]() -(2+x)=-
-(2+x)=-![]() x2+3x-
x2+3x-![]() .
.
要不亏损,应使-![]() x2+3x-
x2+3x-![]() ≥0,得1≤x≤4.
≥0,得1≤x≤4.
当x>4时,利润为7.5-(2+x)=5.5-x.
要不亏损,应使5.5-x≥0,得4<x≤5.5.
综上,要不亏损,产量x(百台)应控制在1≤x≤5.5.
(2)当0≤x≤4时,利润为
-![]() x2+3x-
x2+3x-![]() =-
=-![]() (x-3)2+2;
(x-3)2+2;
当x=3时,利润有最大值2(万元);
当x>4时,利润5.5-x<1.5.
综上,产量为3百台时可使利润最大.
(3)售价为![]() ,当x=3时,产品售价为
,当x=3时,产品售价为
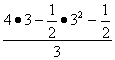 =
=![]() ≈2.33.
≈2.33.
∴产品利润最大时,每百台的售价约为2.33万元.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
| 1 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com