
| A. | m≤-$\frac{3}{2}$ | B. | m≤-3 | C. | m≤-$\frac{2}{3}$ | D. | m≤-$\frac{3}{4}$ |
分析 根据函数f(x)=a|x|(a>0,a≠1)在区间(-∞,0)上为增函数,得到函数为偶函数,且0<a<1,求出函数f(x)的表达式,然后将不等式f(x+m)≤f2(x)化简,对m进行讨论,将x解出来,做到参数分离,由恒成立思想,即可求出m的范围.
解答 解:函数f(x)=a|x|(a>0,a≠1)在区间(-∞,0)上为增函数,
∴f(x)为R上的偶函数,且0<a<1,
∴f(x)=a|x|(x∈R),
∵f(x+m)≤f2(x),
∴a|x+m|≤a|2x|,
∴|x+m|≥|2x|,即(3x+m)(x-m)≤0,当m≤0时,m≤x≤-$\frac{1}{3}$m,
由于对任意的x∈[m,m+l],不等式f(x+m)≤f2(x)恒成立,
∴m≤m且m+1≤-$\frac{1}{3}$m,解得m≤-$\frac{3}{4}$;
当m>0时,-$\frac{m}{3}$≤x≤m,
∴-$\frac{m}{3}$≤m,且m+1≤m,m无解,
综上可知,实数a的取值范围是:m≤-$\frac{3}{4}$;
故选:D.
点评 本题主要考查函数的奇偶性及运用,求出函数在定义域上的解析式是解题的关键,考查解决恒成立问题的常用方法:参数分离,必须掌握.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
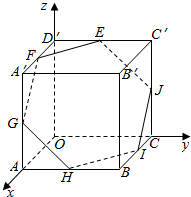 正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.
正方体OABC-D′A′B′C′的棱长为a,E,F,G,H,I,J分别是棱C′D′,D′A′,A′A,AB,BC,CC′的中点,写出正六边形EFGHIJ各顶点的坐际.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四边形ABCD为等腰梯形,PD⊥平面ABCD,F为PC的中点,CD=AD=PD,AB=4AE=2CD=4.
如图,四边形ABCD为等腰梯形,PD⊥平面ABCD,F为PC的中点,CD=AD=PD,AB=4AE=2CD=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com