
分析 设P(t,0),利用圆的切线性质得出|PA|,sin∠APO.使用二倍角公式计算cos∠APB,代入向量的定义式得出$\overrightarrow{PA}•\overrightarrow{PB}$关于t的函数,利用不等式得出数量积的最小值.
解答 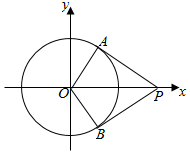 解:∵PA,PB是圆O的切线,
解:∵PA,PB是圆O的切线,
∴|PA|=|PB|,∠APO=∠BPO,
设P(t,0),则t>1.
∴|PA|=|PB|=$\sqrt{{t}^{2}-1}$,sin∠APO=$\frac{1}{t}$,
∴cos∠APB=1-2sin2∠APO=1-$\frac{2}{{t}^{2}}$.
∴$\overrightarrow{PA}•\overrightarrow{PB}$=|PA||PB|cos∠APB=(t2-1)(1-$\frac{2}{{t}^{2}}$)=t2-3+$\frac{2}{{t}^{2}}$≥2$\sqrt{2}$-3.(当且仅当t2=$\frac{2}{{t}^{2}}$,即t2=$\sqrt{2}$时取等号)
∴$\overrightarrow{PA}•\overrightarrow{PB}$的最小值为2$\sqrt{2}-3$.
点评 本题考查了平面向量的数量积运算,圆的切线的性质,属于中档题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [-1,0) | B. | (-1,0) | C. | (-1,+∞) | D. | (-∞,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2a)∪(3a,+∞) | B. | (-∞,3a)∪(-2a,+∞) | C. | (-2a,3a) | D. | (3a,-2a) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M2>N | B. | M2<N | C. | M>N | D. | M<N |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是某赛季甲、乙两名篮球运动员得分情况的茎叶图,从此图可看出甲、乙两人得分的中位数为( )
如图是某赛季甲、乙两名篮球运动员得分情况的茎叶图,从此图可看出甲、乙两人得分的中位数为( )| A. | 31,26 | B. | 26,23 | C. | 36,26 | D. | 31,23 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于原点对称 | B. | 关于点($\frac{π}{6}$,0)对称 | ||
| C. | 关于y轴对称 | D. | 关于直线x=$\frac{π}{6}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com