练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数是定义在上的奇函数，且当时， ，则对任意，函数的零点个数至多有（ ）

    A. 3个 B. 4个 C. 6个 D. 9个

    【答案】A

    【解析】当时,由此可知在上单调递减，在上单调递增， , 且,数是定义在上的奇函数， ，而时， ,所以的图象如图，令,则，由图可知，当时方程至多3个根，当时方程没有根，而对任意， 至多有一个根，从而函数的零点个数至多有3个.

    点晴:本题考查函数导数与单调性.确定零点的个数问题：可利用数形结合的办法判断交点个数，如果函数较为复杂，可结合导数知识确定极值点和单调区间从而确定其大致图象.方程的有解问题就是判断是否存在零点的问题，可参变分离，转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题，往往可利用参变分离的方法，转化为求函数最值处理．也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在正方体ABCD﹣A1B1C1D1中，M和N分别为BC、C1C的中点，那么异面直线MN与AC所成的角等于（ ）
    A.30°
    B.45°
    C.60°
    D.90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）= sin（ωx+φ）﹣cos（ωx+φ）（0＜φ＜π，ω＞0）对任意x∈R，都有f（﹣x）+f（x）=0，f（x）+f（x+ ）=0，则f（ ）=（ ）
    A.0
    B.1
    C.
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设向量 =（sinx，cosx）， =（cosx，sinx），x∈R，函数f（x）= （ ﹣ ）．
    （1）求函数f（x）的最小正周期；
    （2）当x∈[- ， ]时，求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校从高一年级期末考试的学生中抽出60名学生，其成绩（均为整数）的频率分布直方图如图所示：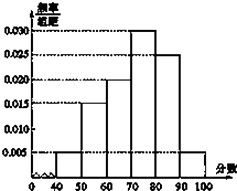
    （1）依据频率分布直方图，估计这次考试的及格率（60分及以上为及格）和平均分；
    （2）已知在[90，100]段的学生的成绩都不相同，且都在94分以上，现用简单随机抽样方法，从95，96，97，98，99，100这6个数中任取2个数，求这2个数恰好是两个学生的成绩的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有以下四种变换方式：

    ① 向左平移个单位长度，再将每个点的横坐标缩短为原来的;

    ② 向右平移个单位长度，再将每个点的横坐标缩短为原来的;

    ③ 每个点的横坐标缩短为原来的，向右平移个单位长度;

    ④ 每个点的横坐标缩短为原来的，向左平移个单位长度;

    其中能将的图像变换成函数的图像的是（ ）

    A.①和③ B.①和④ C.②和④ D.②和③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列函数在（0，+∞）上为减函数的是（ ）
    A.y=﹣|x﹣1|
    B.y=ex
    C.y=ln（x+1）
    D.y=﹣x（x+2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图, 在△中, 点在边上, .

    （Ⅰ）求；

    （Ⅱ）若△的面积是, 求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．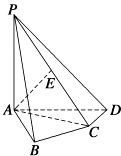
    （1）求PB和平面PAD所成的角的大小；
    （2）证明：AE⊥平面PCD；
    （3）求二面角A﹣PD﹣C得到正弦值．

    查看答案和解析>>

    同步练习册答案