
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的短轴长为
的短轴长为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .当
.当![]() 与
与![]() 连线的斜率为
连线的斜率为![]() 时,直线
时,直线![]() 的倾斜角为
的倾斜角为![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是以
是以![]() 为直径的圆上的任意一点,求证:
为直径的圆上的任意一点,求证:![]()
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() ,g(x)=x2﹣1.
,g(x)=x2﹣1.
(1)求f(x)在点(0,f(0))处的切线方程.
(2)若h(x)=f(x)+g(x)有两个极值点x1,x2(x1<x2),求证:x1f(x1)>x2f(x2).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆的一个顶点为![]() ,焦点在
,焦点在![]() 轴上,中心在原点.若椭圆短轴的上顶点
轴上,中心在原点.若椭圆短轴的上顶点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆的标准方程;
(2)若椭圆的下顶点为![]() ,设直线
,设直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题. 该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取![]() 件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表 1是甲流水线样本的频数分布表,如图所示是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表 1是甲流水线样本的频数分布表,如图所示是乙流水线样本的频率分布直方图.
表1 甲流水线样本的频数分布表
质量指标值 | 频数 |
|
|
|
|
|
|
|
|
|
|
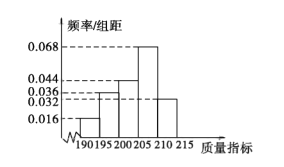
(1)若将频率视为概率,某个月内甲、乙两条流水线均生产了![]() 万件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
万件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(2)在甲流水线抽取的样本的不合格品中随机抽取两件,求两件不合格品的质量指标值均偏大的概率;
(3)根据已知条件完成下面![]() 列联表,并判断在犯错误概率不超过
列联表,并判断在犯错误概率不超过![]() 的前提下能否认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的前提下能否认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络平台从购买该平台某课程的客户中,随机抽取了100位客户的数据,并将这100个数据按学时数,客户性别等进行统计,整理得到如表:
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
(1)根据上表估计男性客户购买该课程学时数的平均值(同一组中的数据用该组区间的中点值作代表,结果保留小数点后两位);
(2)从这100位客户中,对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人,再从这7人中随机抽取2人,求这2人购买的学时数都不低于15的概率.
(3)将购买该课程达到25学时及以上者视为“十分爱好该课程者”,25学时以下者视,为“非十分爱好该课程者”.请根据已知条件完成以下![]() 列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,![]() ,
,![]() ,
,![]() ,
,![]() ,异面直线PA和CD所成角等于60°.
,异面直线PA和CD所成角等于60°.
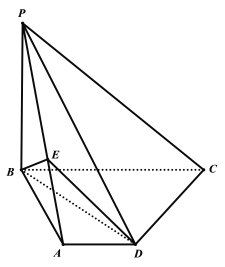
(1)求直线PC和平面PAD所成角的正弦值的大小:
(2)在棱PA上是否存在一点E,使得二面角A-BE-D的余弦值为![]() ?若存在,指出点E在棱PA上的位置;若不存在,说明理由.
?若存在,指出点E在棱PA上的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年7月,中国良渚古城遗址获准列入世界遗产名录,标志着中华五千年文明史得到国际社会认可.良渚古城遗址是人类早期城市文明的范例,实证了中华五千年文明史.考古科学家在测定遗址年龄的过程中利用了“放射性物质因衰变而减少”这一规律.已知样本中碳14的质量N随时间T(单位:年)的衰变规律满足![]() (
(![]() 表示碳14原有的质量),则经过5730年后,碳14的质量变为原来的______;经过测定,良渚古城遗址文物样本中碳14的质量是原来的
表示碳14原有的质量),则经过5730年后,碳14的质量变为原来的______;经过测定,良渚古城遗址文物样本中碳14的质量是原来的![]() 至
至![]() ,据此推测良渚古城存在的时期距今约在5730年到______年之间.(参考数据:
,据此推测良渚古城存在的时期距今约在5730年到______年之间.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com