
分析 用待定系数法求圆的方程,先设出圆的一般方程,因为点A(0,1)和B(4,0)在圆上,满足圆的方程,把两点坐标代入圆方程,又因为圆与x轴相切,所以圆心到x轴的距离等于半径,而这样的圆只有一个,所以由前面几个条件化简得到的方程有唯一解,即可求出圆的方程.
解答 解:设所求圆的方程为x2+y2+Dx+Ey+F=0.
∵点A、B在此圆上,∴E+F+1=0,①,4D+F+16=0②
又知该圆与x轴(直线y=0)相切,令y=0得,x2+Dx+F=0,
∴△=0,即D2-4F=0,③
由①、②、③,解得D=-8,E=-17,F=16.
圆的方程为x2+y2-8x-17y+16=0.
故答案为:x2+y2-8x-17y+16=0.
点评 本题主要考查待定系数法求圆的方程,一般可通过已知条件,设出所求方程,再寻求方程组进行求解.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
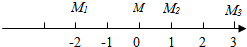 三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)
三台机器人位于同一直线上(如图所示),它们所生产的零件必须逐一送到一个检验台上,经检验合格后,才能送到下一道工序继续加工,已知机器人M1的工作效率是机器人M2的2倍,机器人M2的工作效率是机器人M3的3倍,问检验台放何处最好?(即各机器人到检验台所走距离的总和最小)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com