
分析 (1)先求出从0、2、4、6、8这五个数字中任取2个数字中没有0,能组成没有重复数字的三位数的个数,再求出先求出从0、2、4、6、8这五个数字中任取2个数字中有0,能组成没有重复数字的三位数的个数,由此能求出能组成多少个没有重复数字的三位数.
(2)在(1)中的这260个三位数中,求出能被5整除的有多少个,由此能求出在(1)中的这些三位数中任取一个三位数恰好能被5整除的概率.
解答 解:(1)若从0、2、4、6、8这五个数字中任取2个数字中没有0,
则能组成${C}_{4}^{2}{C}_{5}^{1}{A}_{3}^{3}$=180个没有重复数字的三位数,
若从0、2、4、6、8这五个数字中任取2个数字中有0,
则能组成${C}_{4}^{1}{C}_{5}^{1}×2{{A}_{2}^{2}}_{\;}$=80个没有重复数字的三位数,
∴能组成180+80=260个没有重复数字的三位数.
(2)在(1)中的这260个三位数中,能被5整除的有:${C}_{4}^{1}{C}_{5}^{1}{A}_{2}^{2}$+${C}_{4}^{1}{C}_{4}^{1}{C}_{1}^{1}$=56个,
∴在(1)中的这些三位数中任取一个三位数恰好能被5整除的概率p=$\frac{56}{260}$=$\frac{14}{65}$.
点评 本题考查计数问题及概率的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | [-3,4] | B. | [0,2] | C. | [-$\frac{3}{2}$,$\frac{5}{2}$] | D. | [-4,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
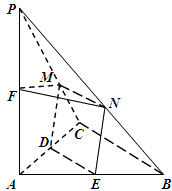 如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=PC=2,AC⊥BC,F为AP的中点,M、N、D、E分别为线段PC、PB、AC、AB上的动点,且MN∥BC∥DE.
如图,在三棱锥P-ABC中,PA⊥平面ABC,2AC=PC=2,AC⊥BC,F为AP的中点,M、N、D、E分别为线段PC、PB、AC、AB上的动点,且MN∥BC∥DE.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com