分析:利用题设条件,先推导出f(0)=0=R,f(x)是奇函数,f(x)在(-1,1)上为单调递减.把
f() 化为 f(
)-f(
),可得P=
f()-f()>
Q=f(),由此能求出P、Q、R的大小关系.
解答:解:∵x∈(-1,1),
f(x)-f(y)=f(),
∴f(0)-f(0)=f(
)=f(0),解得f(0)=0,即 R=f(0)=0.
f(0)-f(x)=f(
)=f(-x),解得f(-x)=-f(x),∴f(x)是奇函数.
∵对任意x∈(-1,0),都有f(x)>0,故当x∈(0,1)时,都有f(x)<0,
Q=f()<0.
令-1<x<y<1,
f(x)-f(y)=f(),∵x-y<0,1-xy>0,∴
<0.
又
+1=
=
,∵1+x>0,1-y>0,1-xy>0,∴
>-1,
∴
f(x)-f(y)=f()>0,∴f(x)在(-1,1)上为单调递减,
从而可得f(
)<
f()<f()<…<f()<…<f()<0,
故
P=f()+f()+…+f()+…+f()<0.
由于
f()=f(
)=f(
)=f(
)+f(
)=f(
)-f(
),
∴
P=f()+f()+…+f()+…+f()=
f()-f()+
f()-f()+
f()-f()+…+
f()-f()=
f()-f().
由于f(
)<0,∴P=
f()-f()>f(
).
综上可得,Q<P<R,
故选D.
点评:本题考查函数的奇偶性和单调性的推导和应用,综合性强,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化,属于难题.



 阅读快车系列答案
阅读快车系列答案![]() )<f(
)<f(![]() ).
). 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.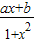 是定义在(-1,1)的奇函数,且f(
是定义在(-1,1)的奇函数,且f( )=
)= .
.