
如图,在二面角αlβ中,A、B∈α,C、D∈l,四边形ABCD为矩形,P∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中点.

(1)求二面角αlβ的大小;
(2)求证:MN⊥AB;
(3)求异面直线PA和MN所成角的大小.
|
(1)解:连结PD,∵四边形ABCD为矩形,∴AD⊥DC,又PA⊥α,∴PD⊥l.∴∠PDA为二面角αlβ的平面角. 又∵PA⊥AD,PA=AD,∴△PAD是等腰直角三角形.∴∠PDA=45°,即二面角αlβ的平面角为45°. (2)证明:过M作ME∥AD,交CD于E,连结NE,则ME⊥CD,NE⊥CD,∴CD⊥平面MNE,MN⊥CD. 又∵AB∥CD,∴MN⊥AB. (3)解:过N作NF∥CD,交PD于F,∵N是PC的中点,∴F是PD的中点.连结AF,可以证明四边形AMNF是平行四边形,∴AF∥MN,∠PAF是异面直线PA和MN所成的角. ∵PA=AD,F是PD的中点.∴AF是∠PAD的角平分线. ∵∠PAD=90°,∴∠PAF=45°.∴异面直线PA和MN所成的角为45°.
|


科目:高中数学 来源: 题型:
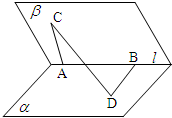 如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若AB=4,AC=6,BD=8,CD=2
如图,在二面角α-l-β的棱l上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,若AB=4,AC=6,BD=8,CD=2| 17 |
查看答案和解析>>
科目:高中数学 来源: 题型:
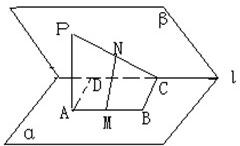 如图:在二面角α-l-β中,A、B∈α,C、D∈l,ABCD为矩形,p∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中点,
如图:在二面角α-l-β中,A、B∈α,C、D∈l,ABCD为矩形,p∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图:在二面角α-l-β中,A、B∈α,C、D∈l,ABCD为矩形,p∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中点,
如图:在二面角α-l-β中,A、B∈α,C、D∈l,ABCD为矩形,p∈β,PA⊥α,且PA=AD,M、N依次是AB、PC的中点,查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省舟山市岱山县大衢中学高二(上)10月月考数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2009-2010学年湖南省岳阳市华容县一中高二(上)期末数学试卷(选修2-1及2-2第一节)(解析版) 题型:填空题
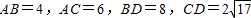 ,则二面角α-l-β的大小为 .
,则二面角α-l-β的大小为 .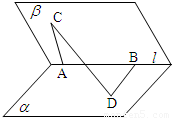
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com