设
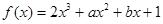
的导数为
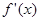
,若函数
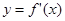
的图象关于直线
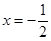
对称,且函数
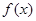
在
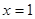
处取得极值.
(I)求实数
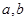
的值;
(II)求函数
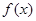
的单调区间.
(I)
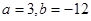
;(II)函数
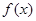
的单调递增区间是
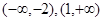
,单调递减区间是
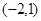
.
试题分析:(I)求导得:
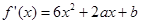
,这是一个二次函数,其对称轴为
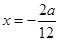
.
由已知条件可得:
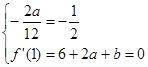
,解这个方程组,可得
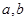
的值.
(II)将
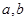
的值代入
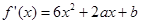
得:
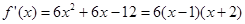
.
由
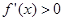
得
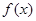
的单调递增区间,由
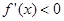
得
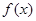
的单调递减区间.
试题解析:(I)求导得:
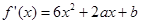
.
依题意有:
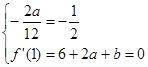
,解得:
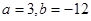
.
(II)由(I)可得:
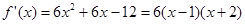
.
令
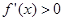
得:
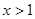
或
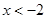
,
令
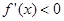
得:
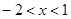
,
综上:函数
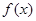
的单调递增区间是
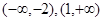
,单调递减区间是
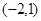
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
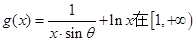
上为增函数,且
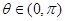
,
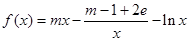
,
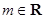
.
(1)求
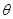
的值;
(2)当
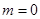
时,求函数
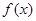
的单调区间和极值;
(3)若在
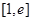
上至少存在一个
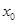
,使得
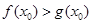
成立,求
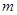
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
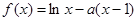
,
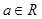
.
(I)讨论函数
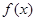
的单调性;
(Ⅱ)当
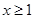
时,
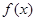
≤
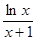
恒成立,求
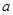
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设
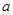
为实数,函数
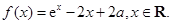
(Ⅰ)求
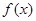
的单调区间与极值;
(Ⅱ)求证:当
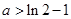
且
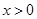
时,
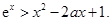
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
函数
f(
x)=
x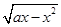
(
a>0)的单调递减区间是________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
定义在R上的函数
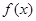
满足:
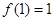
,且对于任意的
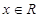
,都有
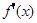
<
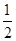
,则不等式
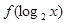
>
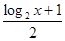
的解集为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若函数
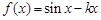
存在极值,则实数
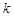
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
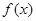
为定义在
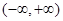
上的可导函数,
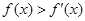
对于
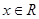
恒成立,且
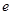
为自然对数的底数,则( )
查看答案和解析>>

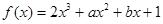 的导数为
的导数为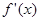 ,若函数
,若函数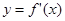 的图象关于直线
的图象关于直线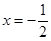 对称,且函数
对称,且函数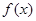 在
在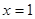 处取得极值.
处取得极值.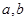 的值;
的值;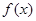 的单调区间.
的单调区间. 阅读快车系列答案
阅读快车系列答案