
分析 原不等式可等价为:arctana-a≤arctanb-b,只需构造函数f(x)=arctanx-x,再运用函数的单调性证明不等式.
解答 证明:∵正切函数y=tanx在(-$\frac{π}{2}$,$\frac{π}{2}$)上单调递增,
∴其反函数y=arctanx在R上也单调递增,
不妨设,a≥b,原不等式可化为:arctana-arctanb≤a-b,
因此,原不等式等价为:arctana-a≤arctanb-b,-----①
要证不等式①成立,只需构造函数,f(x)=arctanx-x,x∈R,
f'(x)=$\frac{1}{1+x^2}$-1=-$\frac{x^2}{1+x^2}$≤0恒成立,
所以,f(x)在R上单调递减,
由于a≥b,所以f(a)≤f(b),
即arctana-a≤arctanb-b,
所以,|arctana-arctanb|≤|a-b|.
说明:本题也可以利用“拉格朗日中值定理”证明.
点评 本题主要考查了运用导数证明不等式,涉及正切,反正切函数的性质,导数的运算,以及函数单调性的确定,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.设AD、PB、PC中点分别为E、F、G.
如图,四棱锥P-ABCD中,底面ABCD为菱形,且PA=PD=DA=2,∠BAD=60°.设AD、PB、PC中点分别为E、F、G.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北冀州市高二理上月考三数学试卷(解析版) 题型:解答题
如图,在底面是直角梯形的四棱锥 中,
中, ,
, 平面
平面 ,
, ,梯形上底
,梯形上底

(1)求证: 平面
平面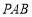 ;
;
(2)求面 与面
与面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com