
分析 (1)An=n2,可得a1=1,n≥2时,an=An-An-1,可得an.由对任意n∈N*,an+1-an=2(bn+1-bn)恒成立.可得bn+1-bn=$\frac{1}{2}$(an+1-an)=1.b1=2,利用等差数列的求和公式即可得出.
(2)Bn+1-Bn=an+1-an=2(bn+1-bn)=bn+1,可得bn+1=2bn,bn=${b}_{1}•{2}^{n-1}$,an=Bn=b1(2n-1).$\frac{{b}_{n+1}}{{a}_{n}{a}_{n+1}}$=$\frac{1}{{b}_{1}}(\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1})$,利用“裂项求和”方法即可得出.
(3)由an+1-an=2(bn+1-bn)=2n+1.n≥2时,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1=2n+1-2.An=2n+2-4-2n.又Bn=2n+1-2.可得$\frac{{A}_{n}}{{B}_{n}}$=2-$\frac{n}{{2}^{n}-1}$.假设存在两个互不相等的整数s,t(1<s<t),使$\frac{{A}_{1}}{{B}_{1}}$,$\frac{{A}_{s}}{{B}_{s}}$,$\frac{{A}_{t}}{{B}_{t}}$成等差数列,等价于$\frac{1}{2-1}$,$\frac{s}{{2}^{s}-1}$,$\frac{t}{{2}^{t}-1}$成等差数列,可得2×$\frac{s}{{2}^{s}-1}$=1+$\frac{t}{{2}^{t}-1}$>1,利用函数的单调性即可判断出结论.
解答 解:(1)∵An=n2,∴a1=1,n≥2时,an=An-An-1=n2-(n-1)2=2n-1,n=1时也成立,∴an=2n-1.
∵对任意n∈N*,an+1-an=2(bn+1-bn)恒成立.
∴bn+1-bn=$\frac{1}{2}$(an+1-an)=1.b1=2,
∴数列{bn}是等差数列,公差为1,首项为2,
∴Bn=2n+$\frac{n(n-1)}{2}×1$=$\frac{1}{2}{n}^{2}$+$\frac{3}{2}$n.
(2)Bn+1-Bn=an+1-an=2(bn+1-bn)=bn+1,可得bn+1=2bn,∴数列{bn}是等比数列,公比为2.
∴bn=${b}_{1}•{2}^{n-1}$,an=Bn=$\frac{{b}_{1}({2}^{n}-1)}{2-1}$=b1(2n-1).
∴$\frac{{b}_{n+1}}{{a}_{n}{a}_{n+1}}$=$\frac{{b}_{1}•{2}^{n}}{{b}_{1}^{2}({2}^{n}-1)({2}^{n+1}-1)}$=$\frac{1}{{b}_{1}}(\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1})$,∴$\frac{{b}_{2}}{{a}_{1}{a}_{2}}$+$\frac{{b}_{3}}{{a}_{2}{a}_{3}}$+$\frac{{b}_{4}}{{a}_{3}a4}$+…+$\frac{{b}_{n+1}}{{a}_{n}{a}_{n+1}}$=$\frac{1}{{b}_{1}}$$[(\frac{1}{2-1}-\frac{1}{{2}^{2}-1})+(\frac{1}{{2}^{2}-1}-\frac{1}{{2}^{3}-1})$+…+$(\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1})]$=$\frac{1}{{b}_{1}}(1-\frac{1}{{2}^{n+1}-1})$<$\frac{1}{3}$成立,
∴b1>$3(1-\frac{1}{{2}^{n+1}-1})$,∴b1≥3.
(3)由an+1-an=2(bn+1-bn)=2n+1.∴n≥2时,an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2n+2n-1+…+22+2=$\frac{2({2}^{n}-1)}{2-1}$=2n+1-2.当n=1时也成立.
∴An=$\frac{4({2}^{n}-1)}{2-1}$-2n=2n+2-4-2n.
又Bn=$\frac{2({2}^{n}-1)}{2-1}$=2n+1-2.∴$\frac{{A}_{n}}{{B}_{n}}$=$\frac{{2}^{n+2}-4-2n}{{2}^{n+1}-2}$=2-$\frac{n}{{2}^{n}-1}$.
假设存在两个互不相等的整数s,t(1<s<t),使$\frac{{A}_{1}}{{B}_{1}}$,$\frac{{A}_{s}}{{B}_{s}}$,$\frac{{A}_{t}}{{B}_{t}}$成等差数列.
等价于$\frac{1}{2-1}$,$\frac{s}{{2}^{s}-1}$,$\frac{t}{{2}^{t}-1}$成等差数列,∴2×$\frac{s}{{2}^{s}-1}$=1+$\frac{t}{{2}^{t}-1}$>1,
∴2×$\frac{s}{{2}^{s}-1}$>1,即2s<2s+1,
令h(s)=2s-2s-1,则h(s+1)-h(s)=2s+1-2(s+1)-1-(2s-2s-1)=2s-2>0,
∴h(s)单调递增,若s≥3,则h(s)≥h(3)=1>0,不满足条件,舍去.
∴s=2,代入得:$\frac{4}{{2}^{2}-1}$=1+$\frac{t}{{2}^{t}-1}$,可得2t-3t-1=0(t≥3).
t=3时不满足条件,舍去.
t≥4时,令u(t)=2t-3t-1=0(t≥4),同理可得函数u(t)单调递增,∴u(t)≥u(4)=3>0,不满足条件.
综上可得:不存在两个互不相等的整数s,t(1<s<t),使$\frac{{A}_{1}}{{B}_{1}}$,$\frac{{A}_{s}}{{B}_{s}}$,$\frac{{A}_{t}}{{B}_{t}}$成等差数列.
点评 本题考查了等差数列与等比数列的通项公式求和公式及其性质、函数的单调性,考查了分类讨论方法、推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
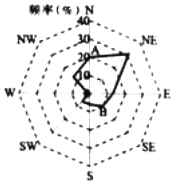 如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )
如图所示为某城市去年风向频率图,图中A点表示该城市去年有的天数吹北风,点表示该城B市去年有10%的天数吹东南风,下面叙述不正确的是( )| A. | 去年吹西北风和吹东风的频率接近 | B. | 去年几乎不吹西风 | ||
| C. | 去年吹东风的天数超过100天 | D. | 去年吹西南风的频率为15%左右 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {2,4} | C. | {2} | D. | {4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com