
分析 根据双曲线的性质分别进行求解判断即可.
解答 解:①以线段F1,F2为直径的圆O的半径R=c,则B(0,c),D(0,c),
则线段BD不是双曲线的虚轴;故①错误,
②∵三角形PF1F2是直角三角形,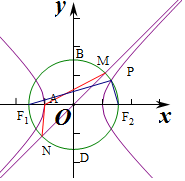
∴PF12+PF22=4c2,
又PF1-PF2=2a,
则平方得PF12+PF22-2PF1PF2=4c2,
即4a2-2PF1PF2=4c2,
则PF1PF2=2c2-2a2=2b2,
则△PF1F2的面积为S=$\frac{1}{2}$PF1PF2=$\frac{1}{2}×$2b2=b2,故②正确,
③由$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}={c}^{2}}\\{y=\frac{b}{a}x}\end{array}\right.$得$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$或$\left\{\begin{array}{l}{x=-a}\\{y=-b}\end{array}\right.$,
即M(a,b),N(-a,-b),
则AN⊥x轴,
若∠MAN=120°,
则∠MAx=30°,
则tan30°=$\frac{b}{2a}$=$\frac{\sqrt{3}}{3}$,平方得$\frac{{b}^{2}}{4{a}^{2}}$=$\frac{1}{3}$,
即$\frac{{b}^{2}}{{a}^{2}}$=$\frac{4}{3}$,
则双曲线C的离心率e=$\frac{c}{a}$=$\sqrt{\frac{{a}^{2}+{b}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{4}{3}}$=$\frac{{\sqrt{21}}}{3}$;故③正确,
④设内切圆与x轴的切点是点H,PF1、PF2分 与内切圆的切点分别为M1、N1,
由双曲线的定义可得|PF1|-|PF2|=2a,由圆的切线长定理知,|PM1|=|PN1|,
故|M1F1|-|N1F2 |=2a,
即|HF1|-|HF2|=2a,设内切圆的圆心横坐标为x,则点H的横坐标为x,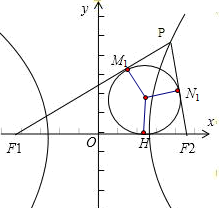
故(x+c)-(c-x)=2a,∴x=a.
即△PF1F2的内切圆的圆心到y轴的距离为a.故④正确,
故答案为:②③④
点评 本题主要考查与双曲线有关的命题的真假判断,涉及双曲线的性质,综合性较强,运算量较大,有一定的难度.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>a>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 1680 | C. | 1344 | D. | 1008 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
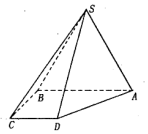 如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.
如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
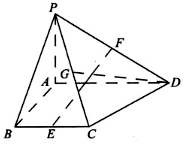 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E,F,G分别为BC,PD,PC的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为直角梯形,AD∥BC,∠BAD=∠CBA=90°,PA=AB=BC=1,AD=2,E,F,G分别为BC,PD,PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com