
����Ŀ����ͼ����������һ��ֱ���õ�Բ�α�־�Բ��ΪC�������ĽӴ���ΪG����Բ�α�־����ͬһƽ���ڵĵ����ϵ�P����һ���۲�㣬��PG=50m���ڹ۲����ǰ��10m������PD=10m����һ����Ϊ10m����ED=10m���Ĺ������ס�����ߣ�����ڹ۲�����ܿ�����Բ�α�־����ּ�Ϊͼ�д�A��F��Բ���� 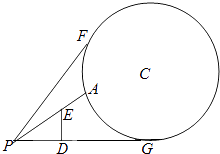
��1����Բ�α�־��뾶Ϊ25m����PG����ֱ��Ϊx�ᣬGΪ����ԭ�㣬����ֱ������ϵ����ԲC��ֱ��PF�ķ��̣�
��2�����ڵ�P���۲��Բ�α�־������ӽǣ�����APF��������ֵΪ ![]() �����Բ�α�־��İ뾶��
�����Բ�α�־��İ뾶��
���𰸡�
��1���⣺ԲC��x2+��y��25��2=252��
ֱ��PB���̣�x��y+50=0��
��ֱ��PF���̣�y=k��x+50����k��0����
��Ϊֱ��PF��ԲC���У����� ![]() �����
����� ![]()
����ֱ��PF���̣� ![]() ����4x��3y+200=0
����4x��3y+200=0
��2���⣺��ֱ��PF���̣�y=k��x+50����k��0����ԲC��x2+��y��r��2=r2��
��Ϊtan��APF=tan����GPF����GPA��= ![]() =
= ![]() ������
������ ![]()
����ֱ��PF���̣� ![]() ����40x��9y+2000=0��
����40x��9y+2000=0��
��Ϊֱ��PF��ԲC���У����� ![]() ��
��
�����2r2+45r��5000=0������2r+125����r��40��=0��
��r=40
����������1������Բ����뾶���ɵ�Բ�ķ��̣�����PF��ԲC���У��ɵ�ֱ��PF�ķ��̣���2�������ֱ��PF���̣�������ֱ��PF��ԲC���У������Բ�α�־��İ뾶��


 ������������Ӧ����ϵ�д�
������������Ӧ����ϵ�д� ͬ����չ�Ķ�ϵ�д�
ͬ����չ�Ķ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Sn������{an}��ǰn��ͣ� ������2Sn=3n+3����{an}��ͨ�ʽ��
������a1=1��an+1��an=2n��n��N*������Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ز�������˾�ƻ���һ¥���ڽ���һ�������ι�ABCD�����ɳ����ε�������A1B1C1D1����Ӱ���֣��ͻ������е���ɣ���֪������A1B1C1D1�����Ϊ4000ƽ���ף����е��Ŀ��ֱ�Ϊ4��10�ף� 
��1�������������ij�A1B1=x�ף���ABCD��ռ���S����x�ĺ���S��x���Ľ���ʽ��
��2��Ҫʹ����ռ�����С��������A1B1C1D1�ij��Ϳ��������ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
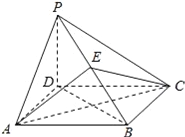
����Ŀ����ͼ������P��ABCD�ĵ����������Σ�PD�͵���ABCD����E����PB�ϣ�
��1����֤��ƽ��AEC��ƽ��PDB��
��2����PD=![]() AB����EΪPB���е�ʱ����AE��ƽ��PDB���ɵĽǵĴ�С��
AB����EΪPB���е�ʱ����AE��ƽ��PDB���ɵĽǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��l1��y=x+a��ֱ��l2��y=x+b��Բ��x��1��2+��y��2��2=8�ֳɳ�����ȵ��Ķλ�����a2+b2= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0������f��x��=acosx+ ![]() +
+ ![]() ������x��[��
������x��[�� ![]() ��
�� ![]() ]��
]��
��1����t= ![]() +
+ ![]() ����t��ȡֵ��Χ������f��x����ʾΪt�ĺ���g��t����
����t��ȡֵ��Χ������f��x����ʾΪt�ĺ���g��t����
��2������f��x�������ֵ��������a��ʾ����
��3����������[�� ![]() ��
�� ![]() ]�ڵ�����x1 �� x2 �� ����|f��x1����f��x2��|��1����ʵ��a��ȡֵ��Χ��
]�ڵ�����x1 �� x2 �� ����|f��x1����f��x2��|��1����ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����M=�� ![]() ��1����
��1���� ![]() ��1����
��1���� ![]() ��1������a+b+c=1������a��0��b��0��c��0������M��ȡֵ��Χ�ǣ� ��
��1������a+b+c=1������a��0��b��0��c��0������M��ȡֵ��Χ�ǣ� ��
A.[0�� ![]() ��
��
B.[ ![]() ��1��
��1��
C.[1��8��
D.[8��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ ![]() =��2��1����
=��2��1���� ![]() =��1��7����
=��1��7���� ![]() =��5��1������R��ֱ��OP�ϵ�һ�㣬����O������ԭ�㣮
=��5��1������R��ֱ��OP�ϵ�һ�㣬����O������ԭ�㣮
��1����ʹ ![]() ȡ����Сֵʱ
ȡ����Сֵʱ ![]() ����������ꣻ
����������ꣻ
��2�����ڣ�1���еĵ�R���� ![]() ��
�� ![]() �нǵ�����ֵ��
�нǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��.
��.
��1����![]() �ڵ�
�ڵ�![]() ����������ֱ��
����������ֱ��![]() ��ֱ����ʵ��
��ֱ����ʵ��![]() ��ֵ��
��ֵ��
��2������![]() �ĵ������䣻
�ĵ������䣻
��3�����ۺ���![]() ������
������![]() �����ĸ���.
�����ĸ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com