
分析 ①由题意作出三角函数线,通过三角形的面积以及扇形面积的大小比较可得.
②作出三角函数线,由三角形两边之和大于第三边可得结论.
解答 解:①在直角坐标系中结合单位圆作出锐角α的正弦线和正切线,
由图可知sinα=MP,α=$\widehat{AP}$,tanα=AT,
∵S△AOP=$\frac{1}{2}$×MP×1=$\frac{1}{2}$sinα,S扇形AOP=$\frac{1}{2}$×$\widehat{AP}$×1=$\frac{1}{2}$α,S△AOT=$\frac{1}{2}$×AT×1=$\frac{1}{2}$tanα,S△AOP<S扇形AOP<S△AOT,
∴MP<$\widehat{AP}$<AT,即sinα<α<tanα,
故答案为:sinα<α<tanα.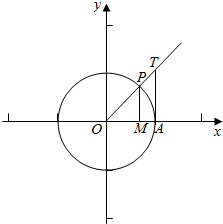
②如图P为α与单位圆交点,
则OP=1,OM、MP分别为α的余弦线,正弦线,
由三角形两边之和大于第三边可得OM+MP>OP,
即sinα+cosα>1.
点评 本题考查三角函数线,考查转化思想以及判断能力,属中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\sqrt{2}$,0) | B. | (-$\sqrt{2}$,$\sqrt{2}$) | C. | (-$\sqrt{2}$,-1) | D. | (-$\sqrt{2}$,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-$\frac{1}{2}$,1) | C. | (-∞,1) | D. | (-$\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com