
分析 (1)欲求在点(1,2)处的切线方程,只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决;
(2)设切点坐标,求出函数的导数,利用导数的几何意义,即可得到结论.
解答 解:由题意y'=2x…(2分)
(1)∵切线的斜率k=2×1=2…(1分)
∴所求切线方程为:y-2=2×(x-1)…(1分)
即2x-y=0…(1分)
(2)设切点$({x_0},{x_0}^2+1)$,则切线斜率k=2x0…(1分),
∴切线方程为:$y-({x_0}^2+1)=2{x_0}•(x-{x_0})$…(1分)
又切线过点(1,1)∴$1-({x_0}^2+1)=2{x_0}•(1-{x_0})$…(1分)
∴x0=0或x0=2…(1分)
∴所求切线方程为y-1=0或y-5=4•(x-2)…(2分)
即y=1或4x-y-3=0…(1分)
点评 本题主要考查导数的几何意义,根据条件求出对应的切线斜率和切点坐标是解决本题的关键,注意过点的切线和在点的切线之间的区别.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | $\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:2:3 | B. | sin1:sin2:sin3 | C. | 1:$\sqrt{3}$:2 | D. | 1:2:$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
| A. | 回归直线一定过点(4.5,3.5) | |
| B. | 工作年限与平均月薪呈正相关 | |
| C. | t的取值是3.5 | |
| D. | 工作年限每增加1年,工资平均提高700元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
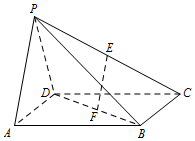 在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.
在四棱锥中P-ABCD,底面ABCD是正方形,侧面PAD⊥底面ABCD,且PA=PD=$\sqrt{2}$,PA⊥PD,E,F分别为PC,BD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 月份x | 1 | 2 | 3 | 4 |
| 用水量 | 4.5 | 4 | 3 | 2.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{99}$ | B. | $\sqrt{33}$ | C. | 4$\sqrt{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com