
【题目】已知四棱锥![]() ,四边形
,四边形![]() 是正方形,
是正方形, ![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.

【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)由![]() 可得
可得![]() ,即
,即![]() ,由
,由![]() 为正方形,可得
为正方形,可得![]() ,从而得
,从而得![]() 平面
平面![]() ,由面面垂直的判定定理可得平面
,由面面垂直的判定定理可得平面![]() 平面
平面![]() ;(2)设
;(2)设![]() 的中点为
的中点为![]() ,∵
,∵![]() ,∴
,∴![]() ,面面垂直的性质可得
,面面垂直的性质可得![]() 平面
平面![]() ,在平面
,在平面![]() 内,过
内,过![]() 作直线
作直线![]() ,则
,则![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立空间直角坐标系,分别根据向量垂直数量积为零列方程组求出平面
轴,建立空间直角坐标系,分别根据向量垂直数量积为零列方程组求出平面![]() 与平面
与平面![]() 的一个法向量,根据空间向量夹角余弦公式,可得结果.
的一个法向量,根据空间向量夹角余弦公式,可得结果.
试题解析:(1)∵![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() 为正方形,∴
为正方形,∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)
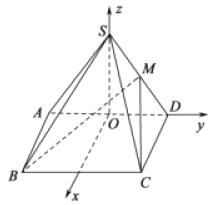
设![]() 的中点为
的中点为![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
由(1)可知平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
在平面![]() 内,过
内,过![]() 作直线
作直线![]() ,则
,则![]() 两两垂直.
两两垂直.
以![]() 为坐标原点,
为坐标原点, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则 ,
,
∴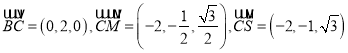 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,
, 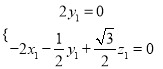 ,即
,即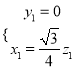 ,取
,取![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,
, 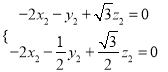 ,即
,即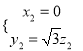 ,取
,取![]() ,
,
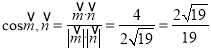 ,由图可知,二面角
,由图可知,二面角![]() 的余弦值为
的余弦值为![]() .
.
【方法点晴】本题主要考查面面垂直的判定定理以及利用空间向量求二面角,属于难题.空间向量解答立体几何问题的一般步骤是:(1)观察图形,建立恰当的空间直角坐标系;(2)写出相应点的坐标,求出相应直线的方向向量;(3)设出相应平面的法向量,利用两直线垂直数量积为零列出方程组求出法向量;(4)将空间位置关系转化为向量关系;(5)根据定理结论求出相应的角和距离.


科目:高中数学 来源: 题型:
【题目】下列函数中与f(x)=x是同一函数的有( )
①y=![]() ②y=
②y=![]() ③y=
③y=![]() ④y=
④y=![]() ⑤f(t)=t⑥g(x)=x
⑤f(t)=t⑥g(x)=x
A. 1 个 B. 2 个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(xy)=f(x)+f(y).
(1) 若x,y∈R,求f(1),f(-1)的值; (2)若x,y∈R,判断y=f(x)的奇偶性;
(3)若函数f(x)在其定义域(0,+∞)上是增函数,f(2)=1,f(x)+f(x-2)≤3,求x的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市“招手即停”公共汽车的票价按下列规则制定:
5公里以内(含5公里),票价2元;
5公里以上,每增加5公里,票价增加1元(不足5公里的按5公里计算).如果某条线路的总里程为20公里,请根据题意.
(1)写出票价与里程之间的函数解析式;
(2)根据(1)写出的函数解析式试画出该函数的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两个随机变量x,y的取值表为
x | 0 | 1 | 3 | 4 |
y | 2.2 | 4.3 | 4.8 | 6.7 |
若x,y具有线性相关关系,且 ![]() =
= ![]() x+2.6,则下列四个结论错误的是( )
x+2.6,则下列四个结论错误的是( )
A.x与y是正相关
B.当x=6时,y的估计值为8.3
C.x每增加一个单位,y增加0.95个单位
D.样本点(3,4.8)的残差为0.56
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱猪ABCD﹣A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,A1A=AB=2,E为棱AA1的中点.
(1)证明:B1C1⊥CE;
(2)求二面角B1﹣CE﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 与点
与点![]() 的距离比它的直线
的距离比它的直线![]() 的距离小2.
的距离小2.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)![]() 是点
是点![]() 轨迹上互相垂直的两条弦,问:直线
轨迹上互相垂直的两条弦,问:直线![]() 是否经过
是否经过![]() 轴上一定点,若经过,求出该点坐标;若不经过,说明理由.
轴上一定点,若经过,求出该点坐标;若不经过,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若
,若![]() 在
在![]() 上为增函数,则称
上为增函数,则称![]() 为“一阶比增函数”.
为“一阶比增函数”.
(1)若![]() 是“一阶比增函数”,求实数a的取值范围。
是“一阶比增函数”,求实数a的取值范围。
(2)若![]() 是“一阶比增函数”,求证:对任意
是“一阶比增函数”,求证:对任意![]() ,
,![]() ,总有
,总有![]() ;
;
(3)若![]() 是“一阶比增函数”,且
是“一阶比增函数”,且![]() 有零点,求证:关于x的不等式
有零点,求证:关于x的不等式![]() 有解.
有解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的上下两个焦点分别为
的上下两个焦点分别为![]() ,
, ![]() ,过点
,过点![]() 与
与![]() 轴垂直的直线交椭圆
轴垂直的直线交椭圆![]() 于
于![]() 、
、![]() 两点,
两点, ![]() 的面积为
的面积为![]() ,椭圆
,椭圆![]() 的离心力为
的离心力为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)已知![]() 为坐标原点,直线
为坐标原点,直线![]() :
: ![]() 与
与![]() 轴交于点
轴交于点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
, ![]() 两个不同的点,若存在实数
两个不同的点,若存在实数![]() ,使得
,使得![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com