
【题目】随着快递行业的崛起,中国快递业务量惊人,2018年中国快递量世界第一,已连续五年突破五百亿件,完全超越美日欧的总和,稳居世界第一名.某快递公司收取费的标准是:不超过1kg的包裹收费8元;超过1kg的包裹,在8元的基础上,每超过1kg(不足1kg,按1kg计算)需再收4元.
该公司将最近承揽(接收并发送)的100件包裹的质量及件数统计如下(表1):
表1:

公司对近50天每天承揽包裹的件数(在表2中的“件数范围”内取的一个近似数据)、件数范围及天数,列表如下(表2):
表2:

(1)将频率视为概率,计算该公司未来3天内恰有1天揽件数在100~299之间的概率;
(2)①根据表1中最近100件包裹的质量统计,估计该公司对承揽的每件包裹收取快递费的平均值:
②根据以上统计数据,公司将快递费的三分之一作为前台工作人员的工资和公司利润,其余用作其他费用.目前,前台有工作人员5人,每人每天揽件数不超过100件,日工资80元.公司正在考虑是否将前台人员裁减1人,试计算裁员前、后公司每天揽件数的数学期望;若你是公司决策者,根据公司每天所获利润的期望值,决定是否裁减前台工作人员1人?
【答案】(1)![]() (2) ①12 ②应裁减1人
(2) ①12 ②应裁减1人
【解析】
(1)根据独立重复时间概率计算公式,可得未来3天内恰有1天揽件数在100~299之间的概率。
(2) ①求出收件费用与收件质量的函数关系式,再由平均数定义即可求得平均收件费用。
②根据收件数量与收件单价,可分别计算出裁减人员前后的利润,比较即可判断出是否需要裁减人员。
(1) 将频率视为概率,计算该公司未来3天内恰有1天揽件数在100~299之间的概率为独立重复事件
样本中包裹件数在100~299之间的天数为![]() ,频率为
,频率为![]()
所以![]()
(2) ①设收件费用为y,收件质量为x,则
收件费用与收件质量的关系式为y=8+4(x-1)=4x+4
所以每件包裹收取快递费的平均值为
![]()
②根据题意及①,揽件数每增加1,公司快递收入增加12(元)
若不裁员,则每天可揽件的上限为500件,公司每日揽件数情况如下:
包裹件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
实际揽件数(取中值) | 50 | 150 | 250 | 350 | 450 |
频率 | 0.1 | 0.2 | 0.5 | 0.1 | 0.1 |
EY | 50×0.1+150×0.2+250×0.5+350×0.1+450×0.1=240 | ||||
所以公司每日利润的期望值为![]() 元
元
若裁员1人,则每天可揽件的上限为400件,公司每日揽件数情况如下:
包裹件数范围 | 0~100 | 101~200 | 201~300 | 301~400 | 401~500 |
实际揽件数(取中值) | 50 | 150 | 250 | 350 | 400 |
频率 | 0.1 | 0.2 | 0.5 | 0.1 | 0.1 |
EY | 50×0.1+150×0.2+250×0.5+350×0.1+400×0.1=235 | ||||
所以公司每日利润的期望值为![]() 元
元
因为560<620 ,所以公司应将前台工作人员裁员1人。


科目:高中数学 来源: 题型:
【题目】已知定点![]() ,动点
,动点![]() 异于原点
异于原点![]() 在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且
在y轴上运动,连接FP,过点P作PM交x轴于点M,并延长MP到点N,且![]() ,
,![]() .
.
![]() 求动点N的轨迹C的方程;
求动点N的轨迹C的方程;
![]() 若直线l与动点N的轨迹交于A、B两点,若
若直线l与动点N的轨迹交于A、B两点,若![]() 且
且![]() ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() 为参数),
为参数),![]() 是
是![]() 上的动点,且满足
上的动点,且满足![]() (
(![]() 为坐标原点),以原点
为坐标原点),以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系,点
轴的正半轴为极轴建立极坐标系,点![]() 的极坐标为
的极坐标为![]()
(1)求线段![]() 的中点
的中点![]() 的轨迹
的轨迹![]() 的普通方程;
的普通方程;
(2)证明:![]() 为定值,并求
为定值,并求![]() 面积的最大值。
面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形ADEF与梯形ABCD所在的平面互相垂直,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,M为CE的中点,N为CD中点.
,M为CE的中点,N为CD中点.
![]() 求证:平面
求证:平面![]() 平面ADEF;
平面ADEF;
![]() 求证:平面
求证:平面![]() 平面BDE;
平面BDE;
![]() 求点D到平面BEC的距离.
求点D到平面BEC的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在人群流量较大的街道,有一中年人吆喝“送钱”,只见他手拿一黑色小布袋,袋中有3只黄色、3只白色的乒乓球(其体积、质地完成相同),旁边立着一块小黑板写道:
摸球方法:从袋中随机摸出3个球,若摸得同一颜色的3个球,摊主送给摸球者5元钱;若摸得非同一颜色的3个球,摸球者付给摊主1元钱.
(1)摸出的3个球为白球的概率是多少?
(2)摸出的3个球为2个黄球1个白球的概率是多少?
(3)假定一天中有100人次摸奖,试从概率的角度估算一下这个摊主一个月(按30天计)能赚多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表,
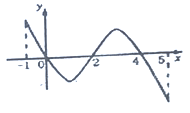
,部分对应值如下表,![]() 的导函数
的导函数![]() 的图象如图所示,给出关于
的图象如图所示,给出关于![]() 的下列命题:
的下列命题:
①函数![]() 在
在![]() 处取得极小值;
处取得极小值;
②函数![]() 在
在![]() 是减函数,在
是减函数,在![]() 是增函数;
是增函数;
③当![]() 时,函数
时,函数![]() 有4个零点;
有4个零点;
④如果当![]() 时,
时,![]() 的最大值是2,那么
的最大值是2,那么![]() 的最小值为0.
的最小值为0.
其中所有的正确命题是__________(写出正确命题的序号).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}为递增的等差数列,数列{bn}满足bn=anan+1an+2(n∈N*),设Sn为数列{bn}的前n项和,若a2![]() ,则当Sn取得最小值时n的值为( )
,则当Sn取得最小值时n的值为( )
A.14B.13C.12D.11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com