
【题目】已知![]() ,
,![]() .
.
(1)当![]() 时,证明:
时,证明:![]() ;
;
(2)已知点![]() ,点
,点![]() ,O为坐标原点,函数
,O为坐标原点,函数![]() ,请判断:当
,请判断:当![]() 时
时![]() 的零点个数.
的零点个数.
【答案】(1)见解析(2)![]() 在
在![]() 上零点个数为2.
上零点个数为2.
【解析】
(1)不等式等价![]() ,设
,设![]() ,计算其导函数的最值得到函数的单调区间,计算最值得到答案.
,计算其导函数的最值得到函数的单调区间,计算最值得到答案.
(2)计算得到函数表达式,求导,讨论![]() ,
,![]() ,
,![]() ,
,![]() 四种情况,根据函数单调性分别计算零点得到答案.
四种情况,根据函数单调性分别计算零点得到答案.
(1)![]() 等价于证明
等价于证明![]() .
.
令![]() ,则
,则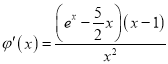 .
.
令![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
∴![]() ,
,
∴![]() 在
在![]() 上恒成立.
上恒成立.
∵![]() 在
在![]() 递减,在
递减,在![]() 递增,∴
递增,∴![]() ,∴
,∴![]() .
.
(2)点![]() ,点
,点![]() ,
,![]() ,
,
∴![]() .
.
①当![]() 时,可知
时,可知![]() ,即
,即![]() ,又
,又![]() ,
,![]() ,
,
∴![]() ,
,![]() 在
在![]() 单调递减.又∵
单调递减.又∵![]() ,
,![]() .
.
∴![]() 在
在![]() 上有一个零点.
上有一个零点.
②当![]() 时,设
时,设![]() ,则
,则![]() ,函数单调递增,
,函数单调递增,
故![]() ,故
,故![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上无零点.
上无零点.
③当![]() 时,∵
时,∵![]() ,
,
∴![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
又∵![]() ,
,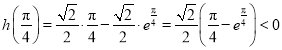 ,
,
∴![]() 在
在![]() 上存在一个零点.
上存在一个零点.
④当![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() 恒成立,
恒成立,
∴![]() 在
在![]() 无零点.
无零点.
综上,![]() 在
在![]() 上零点个数为2.
上零点个数为2.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1,E,F分别是棱CC1,AB的中点.
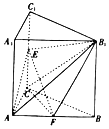
(1)证明:CF∥平面AEB1.
(2)若AC=BC=AA1=4,∠ACB=90°,求三棱锥B1﹣ECF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,.
,.![]() .,
.,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …的前n项和为
…的前n项和为![]() ,正整数
,正整数![]() ,
,![]() 满足:①
满足:①![]() ,②
,②![]() 是满足不等式
是满足不等式![]() 的最小正整数,则
的最小正整数,则![]() ( )
( )
A.6182B.6183C.6184D.6185
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com