
【题目】设函数fn(x)=xn+bx+c(n∈N* , b,c∈R)
(Ⅰ)设n≥2,b=1,c=﹣1,证明:fn(x)在区间( ![]() )内存在唯一的零点;
)内存在唯一的零点;
(Ⅱ)设n=2,若对任意x1 , x2∈[﹣1,1],均有|f2(x1)﹣f2(x2)丨≤4,求b的取值范围.
【答案】解:(Ⅰ)n≥2,b=1,c=﹣1时,fn(x)=xn+x﹣1,
∵ ![]() fn(1)=
fn(1)= ![]() <0,
<0,
∴fn(x)在区间( ![]() )内存在零点,
)内存在零点,
又 ![]() +1>0,
+1>0,
∴fn(x)在区间( ![]() ,1)上是单调递增函数,
,1)上是单调递增函数,
故fn(x)在区间( ![]() )内存在唯一的零点;
)内存在唯一的零点;
(Ⅱ)当n=2时, ![]() ,
,
对任意的x1 , x2∈[﹣1,1],均有|f2(x1)﹣f2(x2)丨≤4等价于f2(x)在[﹣1,1]上的最大值与最小值之差M=f(x)max﹣f(x)min≤4,
据此分类讨论如下:
①当| ![]() |>1,即|b|>2时,M=|f2(1)﹣f2(﹣1)|=2|b|>4,与题设矛盾;
|>1,即|b|>2时,M=|f2(1)﹣f2(﹣1)|=2|b|>4,与题设矛盾;
②当﹣1 ![]() <0,即0<b≤2时,M=
<0,即0<b≤2时,M= ![]() =
= ![]() ≤4恒成立;
≤4恒成立;
②当0<﹣ ![]() ,即﹣2≤b≤0时,M=
,即﹣2≤b≤0时,M= ![]() =
= ![]() 恒成立;
恒成立;
综上知﹣2≤b≤2
【解析】(Ⅰ)表示出fn(x),根据零点判定定理可得函数在区间( ![]() )内存在零点,利用导数可判断函数单调,从而可得零点的唯一性;(Ⅱ)对任意的x1 , x2∈[﹣1,1],均有|f2(x1)﹣f2(x2)丨≤4等价于f2(x)在[﹣1,1]上的最大值与最小值之差M=f(x)max﹣f(x)min≤4,按照对称轴在区间[﹣′1,1]的外边、内部进行分类讨论,可得函数的最大值、最小值及最大值与最小值的差.
)内存在零点,利用导数可判断函数单调,从而可得零点的唯一性;(Ⅱ)对任意的x1 , x2∈[﹣1,1],均有|f2(x1)﹣f2(x2)丨≤4等价于f2(x)在[﹣1,1]上的最大值与最小值之差M=f(x)max﹣f(x)min≤4,按照对称轴在区间[﹣′1,1]的外边、内部进行分类讨论,可得函数的最大值、最小值及最大值与最小值的差.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明. 下面是赵爽的弦图及注文,弦图是一个以勾股之弦为边的正方形,其面积称为弦实.图中包含四个全等的勾股形及一个小正方形,分别涂成红(朱)色及黄色,其面积称为朱实、黄实,利用![]() 勾
勾![]() 股+(股-勾)
股+(股-勾)![]() 朱实+黄实=弦实,化简,得勾2+股2=弦2. 设勾股形中勾股比为
朱实+黄实=弦实,化简,得勾2+股2=弦2. 设勾股形中勾股比为![]() ,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )
,若向弦图内随机抛掷1000颗图钉(大小忽略不计),则落在黄色图形内的图钉数大约为( )

A. 134 B. 866 C. 300 D. 500
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”. 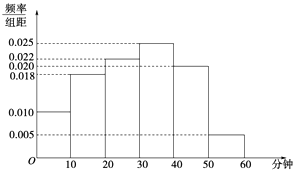
(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | 10 | 55 | |
合计 |
(2)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中,采用随机抽样方法每次抽取1名观众,抽取3次,记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方差D(X).
P(K2≥k) | 0.05 | 0.01 |
k | 3.841 | 6.635 |
附:K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数y=f(x)的定义域为D,若对于任意x1、x2∈D,当x1+x2=2a时,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究函数f(x)=x+sinπx﹣3的某一个对称中心,并利用对称中心的上述定义,可得到f( ![]() )+f(
)+f( ![]() )+…+f(
)+…+f( ![]() )+f(
)+f( ![]() )的值为( )
)的值为( )
A.4027
B.﹣4027
C.8054
D.﹣8054
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准![]() (吨),用水量不超过
(吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ,
, ![]() ,…,
,…, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
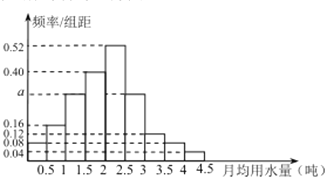
(Ⅰ)求直方图中![]() 的值;
的值;
(Ⅱ)已知该市有80万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使![]() 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由;
的值,并说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域为![]() 的函数
的函数![]() ,如果存在区间
,如果存在区间![]() (
(![]() ),同时满足:
),同时满足:
①![]() 在
在![]() 内是单调函数;②当定义域是
内是单调函数;②当定义域是![]() 时,
时, ![]() 的值域也是
的值域也是![]() .
.
则称函数![]() 是区间
是区间![]() 上的“保值函数”.
上的“保值函数”.
(1)求证:函数![]() 不是定义域
不是定义域![]() 上的“保值函数”;
上的“保值函数”;
(2)已知![]() (
(![]() )是区间
)是区间![]() 上的“保值函数”,求
上的“保值函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com