
【题目】在如图的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 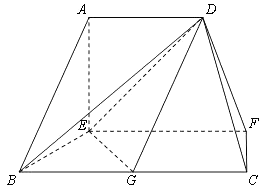
(1)求证:AB∥平面DEG;
(2)求证:BD⊥EG;
(3)求二面角C﹣DF﹣E的余弦值.
【答案】
(1)证明:∵AD∥EF,EF∥BC,∴AD∥BC. 又∵BC=2AD,G是BC的中点,
∴ ![]() ,
,
∴四边形ADGB是平行四边形,∴AB∥DG.∵AB平面DEG,DG平面DEG,∴AB∥平面DEG.
(2)证明:∵EF⊥平面AEB,AE平面AEB,∴EF⊥AE,又AE⊥EB,EB∩EF=E,EB,EF平面BCFE,
∴AE⊥平面BCFE. 过D作DH∥AE交EF于H,则DH⊥平面BCFE.∵EG平面BCFE,∴DH⊥EG.
∵AD∥EF,DH∥AE,∴四边形AEHD平行四边形,∴EH=AD=2,∴EH=BG=2,又EH∥BG,EH⊥BE,
∴四边形BGHE为正方形,∴BH⊥EG. 又BH∩DH=H,BH平面BHD,DH平面BHD,∴EG⊥平面BHD.
∵BD平面BHD,∴BD⊥EG.
(3)解:分别以 EB、EF、EA为x轴、y轴、z轴,建立空间坐标系,由已知得 ![]()
是平面EFDA的法向量.设平面DCF的法向量为n=(x,y,z),∵ ![]() ,
,
∴ 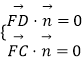 ,即
,即 ![]() ,令z=1,得n=(﹣1,2,1). 设二面角C﹣DF﹣E的大小为θ,
,令z=1,得n=(﹣1,2,1). 设二面角C﹣DF﹣E的大小为θ,
则 ![]() ,∴二面角C﹣DF﹣E的余弦值为
,∴二面角C﹣DF﹣E的余弦值为 ![]() .
.
【解析】(1) 先证明四边形ADGB是平行四边形,可得AB∥DG,从而证明AB∥平面DEG.(2) 过D作DH∥AE交EF于H,则DH⊥平面BCFE,DH⊥EG,再证BH⊥EG,从而可证EG⊥平面BHD,故BD⊥EG.(3)分别以 EB、EF、EA为x轴、y轴、z轴,建立空间坐标系,由已知得 ![]() 是平面EFDA的法向量.
是平面EFDA的法向量.
求出平面DCF的法向量为n=(x,y,z),则由 ![]() 求得 二面角C﹣DF﹣E的余弦值.
求得 二面角C﹣DF﹣E的余弦值.
【考点精析】通过灵活运用直线与平面平行的判定和直线与平面垂直的性质,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;垂直于同一个平面的两条直线平行即可以解答此题.


科目:高中数学 来源: 题型:
【题目】某校从高一年级A,B两个班中各选出7名学生参加物理竞赛,他们的成绩(单位:分)的茎叶图如图所示,其中A班学生的平均分是85分 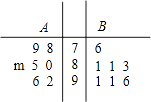
(1)求m的值,并计算A班7名学生成绩的方差s2;
(2)从成绩在90分以上的学生中随机抽取两名学生,求至少有一名A班学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱柱ABCD﹣A1B1C1D1中,底面ABCD是梯形,AD∥BC,侧面ABB1A1为菱形,∠DAB=∠DAA1 . 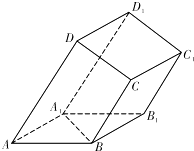
(Ⅰ)求证:A1B⊥BC;
(Ⅱ)若AD=AB=3BC,∠A1AB=60°,点D在平面ABB1A1上的射影恰为线段A1B的中点,求平面DCC1D1与平面ABB1A1所成锐二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知向量 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),
), ![]() =(sinx,cosx),x∈(0,
=(sinx,cosx),x∈(0, ![]() ).
).
(1)若 ![]() ⊥
⊥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() 与
与 ![]() 的夹角为
的夹角为 ![]() ,求x的值.
,求x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3+ax2+bx+
x3+ax2+bx+ ![]() (a,b是实数),且f′(2)=0,f(﹣1)=0.
(a,b是实数),且f′(2)=0,f(﹣1)=0.
(1)求实数a,b的值;
(2)当x∈[﹣1,t]时,求f(x)的最大值g(t)的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,
, ![]() 为椭圆
为椭圆![]() 的右顶点,
的右顶点, ![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的上、下顶点.线段
的上、下顶点.线段![]() 的延长线与线段
的延长线与线段![]() 交于点
交于点![]() ,与椭圆
,与椭圆![]() 交于点
交于点![]() .(1)若椭圆的离心率为
.(1)若椭圆的离心率为![]() ,
, ![]() 的面积为12,求椭圆
的面积为12,求椭圆![]() 的方程;(2)设
的方程;(2)设![]() ,求实数
,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在极坐标系(与平面直角坐标系
为参数).在极坐标系(与平面直角坐标系![]() 取相同的长度单位,且以原点
取相同的长度单位,且以原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线![]() 的方程为
的方程为![]() .
.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 是曲线
是曲线![]() 上的任意一点,求点
上的任意一点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com