
【题目】对点![]() 的直线l分別交
的直线l分別交![]() 与
与![]() 于
于![]() 两点.
两点.
(1)设![]() 的面积为
的面积为![]() ,求直线l的方程;
,求直线l的方程;
(2)当![]() 最小时,求直线l的方程.
最小时,求直线l的方程.
【答案】(1)![]() ;
;
(2)![]() .
.
【解析】
(1)设所求直线l的方程,分别与直线![]() 与
与![]() 联立,得出交点A、B的纵坐标,根据三角形的面积公式得出方程,求解可得所求直线的方程;
联立,得出交点A、B的纵坐标,根据三角形的面积公式得出方程,求解可得所求直线的方程;
(2)设直线l的参数式方程,分别代入直线![]() 与
与![]() 中,得出
中,得出![]() 、
、![]() ,从而得出
,从而得出![]() ,运用三角函数的恒等变形得出其最小值,由(1)得出交点的纵坐标可求解出满足题意的值,得出直线的方程.
,运用三角函数的恒等变形得出其最小值,由(1)得出交点的纵坐标可求解出满足题意的值,得出直线的方程.
(1)设![]() ,直线
,直线![]() ,
,
由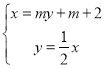 化简得A点的纵坐标
化简得A点的纵坐标![]() ,
,
由![]() ,化简得B点的纵坐标
,化简得B点的纵坐标![]()
![]() ,
,
所以,![]() ,化简得
,化简得![]() ,
,
故直线![]() 的方程为:
的方程为:![]() ;
;
(2)设直线![]() 的倾斜角为
的倾斜角为![]() ,所以直线
,所以直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),
为参数),
将直线![]() 的参数方程分别代入
的参数方程分别代入 ![]() 与
与![]() 得:
得:
![]()
![]() ,
,
所以![]() ,
,
由(1)得![]() ,
,![]() ,
,
当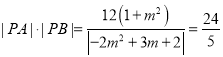 时,化简得
时,化简得![]() 或
或![]() ,解得
,解得![]() 或
或![]() .
.
因为点A在第一象限,所以![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以直线![]() .
.
故得解.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分13分) 已知双曲线![]() 的两个焦点为
的两个焦点为![]() 的曲线C上.
的曲线C上.
(Ⅰ)求双曲线C的方程;
(Ⅱ)记O为坐标原点,过点Q(0,2)的直线l与双曲线C相交于不同的两点E、F,若△OEF的面积为![]() 求直线l的方程
求直线l的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
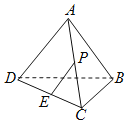
【题目】已知三棱锥A﹣BCD的所有棱长均相等,E为DC的中点,若点P为AC中点,则直线PE与平面BCD所成角的正弦值为_____,若点Q在棱AC所在直线上运动,则直线QE与平面BCD所成角正弦值的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以平面直角坐标系
为参数),以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 上的动点
上的动点![]() 到坐标原点
到坐标原点![]() 的距离
的距离![]() 的最大值;
的最大值;
(Ⅱ)若曲线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,且与
两点,且与![]() 轴相交于点
轴相交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】物价监督部门为调研某公司新开发上市的一种产品销售价格的合理性,对某公司的该产品的销量与价格进行了统计分析,得到如下数据和散点图:
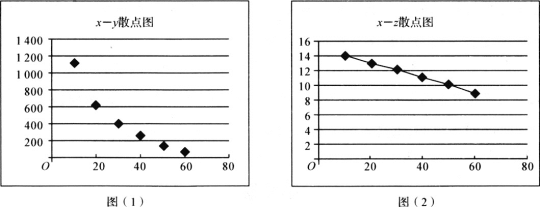
定价x(元/kg) | 10 | 20 | 30 | 40 | 50 | 60 |
年销量y(kg) | 1150 | 643 | 424 | 262 | 165 | 86 |
z=21ny | 14.1 | 12.9 | 12.1 | 11.1 | 10.2 | 8.9 |
(参考数据:![]() ,
,![]() ,
,
![]() ,
,![]() )
)
(Ⅰ)根据散点图判断,y与x和z与x哪一对具有的线性相关性较强(给出判断即可,不必说明理由)?
(Ⅱ)根据(Ⅰ)的判断结果及数据,建立y关于x的回归方程(方程中的系数均保留两位有效数字).
附:对于一组数据(x1,y1),(x2,y2),(x3,y3),…,(xn,yn),其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为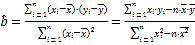 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了茎叶图:则下列结论中表述不正确的是
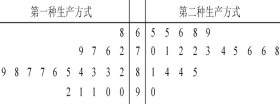
A. 第一种生产方式的工人中,有75%的工人完成生产任务所需要的时间至少80分钟
B. 第二种生产方式比第一种生产方式的效率更高
C. 这40名工人完成任务所需时间的中位数为80
D. 无论哪种生产方式的工人完成生产任务平均所需要的时间都是80分钟.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=
的底面为菱形且∠ABC=120°,PA⊥底面ABCD,AB=1,PA=![]() ,E为PC的中点.
,E为PC的中点.
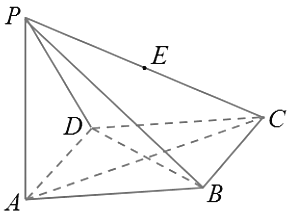
(1)求直线DE与平面PAC所成角的大小;
(2)求二面角E-AD-C平面角的正切值;
(3)在线段PC上是否存在一点M,使PC⊥平面MBD成立.如果存在,求出MC的长;如果不存在,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线C:![]() 1(a>0,b>0)的左右焦点为F1,F2(|F1F2|=2c),以坐标原点O为圆心,以c为半径作圆A,圆A与双曲线C的一个交点为P,若三角形F1PF2的面积为a2,则C的离心率为_____.
1(a>0,b>0)的左右焦点为F1,F2(|F1F2|=2c),以坐标原点O为圆心,以c为半径作圆A,圆A与双曲线C的一个交点为P,若三角形F1PF2的面积为a2,则C的离心率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com