
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c且acosC﹣ ![]() =b.
=b.
(1)求角A的大小;
(2)若a=1,求△ABC的周长的取值范围.
【答案】
(1)解:∵acosC﹣ ![]() =b,
=b,
∴根据正弦定理,得sinAcosC﹣ ![]() sinC=sinB.
sinC=sinB.
又∵△ABC中,sinB=sin(π﹣B)=sin(A+C)=sinAcosC+cosAsinC,
∴sinAcosC﹣ ![]() sinC=sinAcosC+cosAsinC,
sinC=sinAcosC+cosAsinC,
化简得﹣ ![]() sinC=cosAsinC,结合sinC>0可得cosA=﹣
sinC=cosAsinC,结合sinC>0可得cosA=﹣ ![]()
∵A∈(0,π),∴A= ![]()
(2)解:∵A= ![]() ,a=1,
,a=1,
∴根据正弦定理 ![]() ,可得b=
,可得b= ![]() =
= ![]() =
= ![]() sinB,同理可得c=
sinB,同理可得c= ![]() sinC,
sinC,
因此,△ABC的周长l=a+b+c=1+ ![]() sinB+
sinB+ ![]() sinC
sinC
=1+ ![]() [sinB+sin(
[sinB+sin( ![]() ﹣B)]=1+
﹣B)]=1+ ![]() [sinB+(
[sinB+( ![]() cosB﹣
cosB﹣ ![]() sinB)]
sinB)]
=1+ ![]() (
( ![]() sinB+
sinB+ ![]() cosB)=1+
cosB)=1+ ![]() sin(B+
sin(B+ ![]() ).
).
∵B∈(0, ![]() ),得B+
),得B+ ![]() ∈(
∈( ![]() ,
, ![]() )
)
∴sin(B+ ![]() )∈(
)∈( ![]() ,1],可得l=a+b+c=1+
,1],可得l=a+b+c=1+ ![]() sin(B+
sin(B+ ![]() )∈(2,1+
)∈(2,1+ ![]() ]
]
即△ABC的周长的取值范围为(2,1+ ![]() ]
]
【解析】(1)根据正弦定理化简题中等式,得sinAcosC﹣ ![]() sinC=sinB.由三角形的内角和定理与诱导公式,可得sinB=sin(A+C)=sinAcosC+cosAsinC,代入前面的等式解出cosA=﹣
sinC=sinB.由三角形的内角和定理与诱导公式,可得sinB=sin(A+C)=sinAcosC+cosAsinC,代入前面的等式解出cosA=﹣ ![]() ,结合A∈(0,π)可得角A的大小;(2)根据A=
,结合A∈(0,π)可得角A的大小;(2)根据A= ![]() 且a=1利用正弦定理,算出b=
且a=1利用正弦定理,算出b= ![]() sinB且c=
sinB且c= ![]() sinC,结合C=
sinC,结合C= ![]() ﹣B代入△ABC的周长表达式,利用三角恒等变换化简得到△ABC的周长关于角B的三角函数表达式,再根据正弦函数的图象与性质加以计算,可得△ABC的周长的取值范围.
﹣B代入△ABC的周长表达式,利用三角恒等变换化简得到△ABC的周长关于角B的三角函数表达式,再根据正弦函数的图象与性质加以计算,可得△ABC的周长的取值范围.


科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤? (参考数值:3×2.5+4×3+5×4+6×4.5=66.5)计算回归系数 ![]() ,
, ![]() .公式为
.公式为 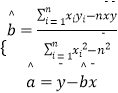 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点
,以极点为原点![]() ,极轴为
,极轴为![]() 轴正半轴(两坐标系取相同的单位长度)的直角坐标系
轴正半轴(两坐标系取相同的单位长度)的直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若用![]() 代换曲线
代换曲线![]() 的普通方程中的
的普通方程中的![]() 得到曲线
得到曲线![]() 的方程,若
的方程,若![]() 分别是曲线
分别是曲线![]() 和曲线
和曲线![]() 上的动点,求
上的动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A、B、C所对的边分别为a,b,c. (Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂定期购买面粉.已知该厂每天需用面粉6t,每吨面粉的价格为1800元,面粉的保管等其他费用为平均每吨每天3元,购面粉每次需支付运费900元.
(1)求该厂多少天购买一次面粉,才能使平均每天所支付的总费用最少?
(2)若提供面粉的公司规定:当一次购买面粉不少于210t时,其价格可享受9折优惠(即原价的90%),问该厂是否考虑利用此优惠条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了考核甲,乙两部门的工作情况,随机访问了50位市民,根据这50位市民对这两部门的评分(评分越高表明市民的评价越高),绘制茎叶图如下:

(1)分别估计该市的市民对甲,乙两部门评分的中位数;
(2)分别估计该市的市民对甲,乙两部门的评分高于90的概率;
(3)根据茎叶图分析该市的市民对甲,乙两部门的评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() (单位:万件)与年促销费用
(单位:万件)与年促销费用![]() (单位:万元)(
(单位:万元)(![]() )满足
)满足![]() (
(![]() 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件.已知2017年生产该产品的固定投入为8万元.每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2017年该产品的利润![]() (单位:万元)表示为年促销费用
(单位:万元)表示为年促销费用![]() (单位:万元)的函数;
(单位:万元)的函数;
(2)该厂家2017年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1,g(x)=﹣x2+4x﹣3,若有f(a)=g(b),则b的取值范围为( )
A.![]()
B.(2﹣ ![]() ,2+
,2+ ![]() )
)
C.[1,3]
D.(1,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com