
【题目】选修4-4,坐标系与参数方程
已知在平面直角坐标系xOy中,椭圆C的方程为![]() ,以O为极点,x轴的非负半轴为极轴,取相同的长度单位建立极坐标系,直线
,以O为极点,x轴的非负半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设M(x,y)为椭圆C上任意一点,求|![]() x+y﹣1|的最大值.
x+y﹣1|的最大值.
【答案】(1)![]() (2)9
(2)9
【解析】试题分析:(1)根据![]() 将直线极坐标方程化为直角坐标方程,(2)根据椭圆参数方程化简|
将直线极坐标方程化为直角坐标方程,(2)根据椭圆参数方程化简|![]() x+y﹣1|,再根据三角函数有界性以及绝对值定义确定函数最大值.
x+y﹣1|,再根据三角函数有界性以及绝对值定义确定函数最大值.
试题解析:(1)根据题意,椭圆C的方程为![]() +
+![]() =1,
=1,
则其参数方程为![]() ,(α为参数);
,(α为参数);
直线l的极坐标方程为ρsin(θ+![]() )=3,变形可得ρsinθcos
)=3,变形可得ρsinθcos![]() +ρcosθsin
+ρcosθsin![]() =3,
=3,
即![]() ρsinθ+
ρsinθ+![]() ρcosθ=3,,将x=ρcosθ,y=ρsinθ代入可得
ρcosθ=3,,将x=ρcosθ,y=ρsinθ代入可得![]() x+y﹣6=0,
x+y﹣6=0,
即直线l的普通方程为![]() x+y﹣6=0;
x+y﹣6=0;
(2)根据题意,M(x,y)为椭圆一点,则设M(2cosθ,4sinθ),
|2![]() x+y﹣1|=|4
x+y﹣1|=|4![]() cosθ+4sinθ﹣1|=|8sin(θ+
cosθ+4sinθ﹣1|=|8sin(θ+![]() )﹣1|,
)﹣1|,
分析可得,当sin(θ+![]() )=﹣1时,|2
)=﹣1时,|2![]() x+y﹣1|取得最大值9.
x+y﹣1|取得最大值9.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
【题目】微信是当前主要的社交应用之一,有着几亿用户,覆盖范围广,及时快捷,作为移动支付的重要形式,微信支付成为人们支付的重要方式和手段。某公司为了解人们对“微信支付”认可度,对![]() 年龄段的人群随机抽取
年龄段的人群随机抽取![]() 人进行了一次“你是否喜欢微信支付”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
人进行了一次“你是否喜欢微信支付”的问卷调查,根据调查结果得到如下统计表和各年龄段人数频率分布直方图:
组号 | 分组 | 喜欢微信支付的人数 | 喜欢微信支付的人数 占本组的频率 |
第一组 |
|
|
|
第二组 |
|
|
|
第三组 |
|
|
|
第四组 |
|
|
|
第五组 |
|
|
|
第六组 |
|
|
|

(1)补全频率分布直方图,并求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)在第四、五、六组“喜欢微信支付”的人中,用分层抽样的方法抽取![]() 人参加“微信支付日鼓励金”活动,求第四、五、六组应分别抽取的人数;
人参加“微信支付日鼓励金”活动,求第四、五、六组应分别抽取的人数;
(3)在(2)中抽取的![]() 人中随机选派
人中随机选派![]() 人做采访嘉宾,求所选派的
人做采访嘉宾,求所选派的![]() 人没有第四组人的概率.
人没有第四组人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村计划建造一个室内面积为800m2的矩形蔬菜温室,在室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地.当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若满足条件:存在
,若满足条件:存在![]() ,使
,使![]() 在
在![]() 上的值域为
上的值域为![]() ,则称
,则称![]() 为“倍缩函数”.若函数
为“倍缩函数”.若函数![]() 为“倍缩函数”,则实数
为“倍缩函数”,则实数![]() 的取值范围是
的取值范围是
A. (﹣∞,ln2﹣1) B. (﹣∞,ln2﹣1]
C. (1﹣ln2,+∞) D. [1﹣ln2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过中央电视台《魅力中国城》栏目的三轮角逐,黔东南州以三轮竞演总分排名第一名问鼎“最具人气魅力城市”.如图统计了黔东南州从2010年到2017年的旅游总人数(万人次)的变化情况,从一个侧面展示了大美黔东南的魅力所在.根据这个图表,在下列给出的黔东南州从2010年到2017年的旅游总人数的四个判断中,错误的是( )
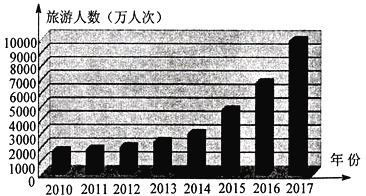
A. 旅游总人数逐年增加
B. 2017年旅游总人数超过2015、2016两年的旅游总人数的和
C. 年份数与旅游总人数成正相关
D. 从2014年起旅游总人数增长加快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆![]() 极坐标方程为
极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求直线
时,求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与圆
与圆![]() 的交点为
的交点为![]() 、
、![]() ,证明:
,证明:![]() 是与
是与![]() 无关的定值.
无关的定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018届北京市海淀区】如图,三棱柱![]() 侧面
侧面![]() 底面
底面![]() ,
, ![]()
![]()
![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
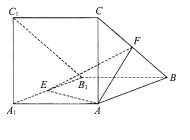
(Ⅰ)求证: ![]() ;
;
(Ⅱ)求三棱柱![]() 的体积;
的体积;
(Ⅲ)在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com