
【题目】已知函数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(1)根据题意,知![]() 的定义域
的定义域![]() ,
,![]() ,分类讨论参数
,分类讨论参数![]() ,当
,当![]() ,
,![]() ,
,![]() 时,利用导数研究函数的单调性;
时,利用导数研究函数的单调性;
(2)由题知![]() ,所以
,所以![]() ,求
,求![]() 时,
时,![]() ,转化为
,转化为![]() ,分类讨论,根据导数研究函数单调性,求出符合
,分类讨论,根据导数研究函数单调性,求出符合![]() 时,实数
时,实数![]() 的取值范围.
的取值范围.
解:(1)![]() 的定义域
的定义域![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() ;
;![]() ,
,![]() ,
,
即![]() 在
在![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,即
,即![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,
,![]() ;
;![]() ,
,![]() 或
或![]() ,
,
即![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,
,![]() ;
;![]() ,
,![]() 或
或![]() ,
,
即![]() 在
在![]() 和
和![]() 上单调递增,
上单调递增,![]() 在
在![]() 上单调递减.
上单调递减.
(2)由题知![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
即![]() 不满足题意;
不满足题意;
当![]() 时,
时,![]() 在
在![]() 单调递增,即
单调递增,即![]() ,符合题意;
,符合题意;
当![]() 时,由(1)得:
时,由(1)得:
当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,
即![]() ,符合题意;
,符合题意;
当![]() 时,即
时,即![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
即![]() ,
,![]() 不合题意,舍去.
不合题意,舍去.
综上可知![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为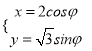 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市垃圾处理厂的垃圾年处理量(单位:千万吨)与资金投入量x(单位:千万元)有如下统计数据:
2012年 | 2013年 | 2014年 | 2015年 | 2016年 | |
资金投入量x(千万元) | 1.5 | 1.4 | 1.9 | 1.6 | 2.1 |
垃圾处理量y(千万吨) | 7.4 | 7.0 | 9.2 | 7.9 | 10.0 |
(1)若从统计的5年中任取2年,求这2年的垃圾处理量至少有一年不低于8.0(千万吨)的概率;
(2)由表中数据求得线性回归方程为![]() ,该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨,现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元,请你预测2017年能否完成垃圾处理任务,若不能,缺口约为多少千万吨?
,该垃圾处理厂计划2017年的垃圾处理量不低于9.0千万吨,现由垃圾处理厂决策部门获悉2017年的资金投入量约为1.8千万元,请你预测2017年能否完成垃圾处理任务,若不能,缺口约为多少千万吨?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月,北京世界园艺博览会开幕,为了保障园艺博览会安全顺利地进行,某部门将5个安保小组全部安排到指定的三个不同区域内值勤,则每个区域至少有一个安保小组的排法有( )
A.150种B.240种C.300种D.360种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从学生会宣传部6名成员(其中男生4人,女生2人)中,任选3人参加某省举办的“我看中国改革开放三十年”演讲比赛活动.
(1)设所选3人中女生人数为ξ,求ξ的分布列;
(2)求男生甲或女生乙被选中的概率;
(3)设“男生甲被选中”为事件A,“女生乙被选中”为事件B,求P(B)和P(B|A).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车站每天上午发出两班客车,每班客车发车时刻和发车概率如下:第一班车:在8:00,8:20,8:40发车的概率分别为![]() ,
,![]() ,
,![]() ;第二班车:在9:00,9:20,9:40发车的概率分别为
;第二班车:在9:00,9:20,9:40发车的概率分别为![]() ,
,![]() ,
,![]() .两班车发车时刻是相互独立的,一位旅客8:10到达车站乘车.求:
.两班车发车时刻是相互独立的,一位旅客8:10到达车站乘车.求:
(1)该旅客乘第一班车的概率;
(2)该旅客候车时间(单位:分钟)的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() ,设
,设![]() ,则以下四个命题:(1)
,则以下四个命题:(1)![]() 是等差数列;(2)
是等差数列;(2)![]() 中最大项是
中最大项是![]() ;(3)
;(3)![]() 通项公式是
通项公式是![]() ;(4)
;(4)![]() .其中真命题的序号是______.
.其中真命题的序号是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com