
���� ��1���������´����ɱ�y��Ԫ�����´�����x���֣�֮��ĺ�����ϵ�ɽ��Ƶı�ʾΪ��y=$\frac{1}{2}$x2-200x+45000������ͬʱ����x��Ȼ�����û�������ʽ�Ӷ������ֵ��
��2����õ�λÿ�»���ΪS����S=200x-y����yֵ������л���Ȼ�������䷽���������
��� �⣺��1���������֪���´����ɱ�y��Ԫ�����´�����x���֣�֮��ĺ�����ϵ�ɽ��Ƶر�ʾΪ$y=\frac{1}{2}{x^2}-200x+45000$��
�������̼ÿ�ֵ�ƽ�������ɱ�Ϊ$\frac{y}{x}=\frac{1}{2}x+\frac{45000}{x}-200$$��2\sqrt{\frac{1}{2}x•\frac{45000}{x}}-200=100$��-----------------��4�֣�
���ҽ���$\frac{1}{2}$x=$\frac{45000}{x}$����x=300ʱ�Ⱥų�����-------------------��5�֣�
�ʸõ�λ�´�����Ϊ300��ʱ������ʹÿ�ֵ�ƽ�������ɱ���ͣ���ͳɱ�Ϊ100Ԫ��----------------------------��6�֣�
��2���õ�λÿ���ܻ�����
��õ�λÿ�»���ΪSԪ����
S=200x-y=-$\frac{1}{2}$x2+400x-45000=-$\frac{1}{2}$��x-400��2+35 000��--------------��9�֣�
��Ϊx��[300��600]������S��[15 000��35 000]��-----------------��11�֣�
�ʸõ�λÿ�»������������Ϊ35000Ԫ��-----------------------��12�֣�
���� ������һ��ʵ��Ӧ���⣬�����˺�������ֵ�ͻ�������ʽ���������䷽����������ֵ��


 һ����������ϵ�д�
һ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | b��a��c | B�� | b��c��a | C�� | a��b��c | D�� | a��c��b |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{\sqrt{15}}{15}$��$\frac{1}{3}$�� | B�� | [$\frac{1}{5}$��$\frac{\sqrt{15}}{15}$�� | C�� | ��$\frac{1}{5}$��$\frac{\sqrt{15}}{15}$] | D�� | ��$\frac{1}{7}$��$\frac{1}{5}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
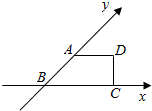 һ��ˮƽ���õ�ƽ��ͼ�ε�б����ֱ��ͼ��ֱ������ABCD����ͼ��ʾ����ABC=45�㣬$AB=AD=\sqrt{2}$��DC��BC�����ƽ��ͼ�ε����Ϊ$4+\sqrt{2}$��
һ��ˮƽ���õ�ƽ��ͼ�ε�б����ֱ��ͼ��ֱ������ABCD����ͼ��ʾ����ABC=45�㣬$AB=AD=\sqrt{2}$��DC��BC�����ƽ��ͼ�ε����Ϊ$4+\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com