
【题目】下列说法中正确的是( )
A.若样本数据![]() ,
,![]() ,…,
,…,![]() 的平均数为5,则样本数据
的平均数为5,则样本数据![]() ,
,![]() ,…,
,…,![]() 的平均数为10
的平均数为10
B.用系统抽样法从某班按学号抽取5名同学参加某项活动,若抽取的学号为5,16,27,38,49,则该班学生人数可能为60
C.某种圆环形零件的外径服从正态分布![]() (单位:
(单位:![]() ),质检员从某批零件中随机抽取一个,测得其外径为
),质检员从某批零件中随机抽取一个,测得其外径为![]() ,则这批零件不合格
,则这批零件不合格
D.对某样本通过独立性检验,得知有![]() 的把握认为吸烟与患肺病有关系,则在该样本吸烟的人群中有
的把握认为吸烟与患肺病有关系,则在该样本吸烟的人群中有![]() 的人可能患肺病
的人可能患肺病
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.

(Ⅰ)证明: BC1//平面A1CD;
(Ⅱ)设AA1= AC=CB=2,AB=2![]() ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两位同学玩游戏,对于给定的实数![]() ,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把
,按下列方法操作一次产生一个新的实数:由甲、乙同时各掷一枚均匀的硬币,如果出现两个正面朝上或两个反面朝上,则把![]() 乘以2后再减去6;如果出现一个正面朝上,一个反面朝上,则把
乘以2后再减去6;如果出现一个正面朝上,一个反面朝上,则把![]() 除以2后再加上6,这样就可得到一个新的实数
除以2后再加上6,这样就可得到一个新的实数![]() ,对实数
,对实数![]() 仍按上述方法进行一次操作,又得到一个新的实数
仍按上述方法进行一次操作,又得到一个新的实数![]() ,当
,当![]() 时,甲获胜,否则乙获胜,若甲胜的概率为
时,甲获胜,否则乙获胜,若甲胜的概率为![]() ,则
,则![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点
).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,直线l的参数方程为![]() (t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(t为参数),曲线C1的方程为ρ(ρ-4sin θ)=12,定点A(6,0),点P是曲线C1上的动点,Q为AP的中点.
(1)求点Q的轨迹C2的直角坐标方程;
(2)直线l与直线C2交于A,B两点,若|AB|≥2![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年12月1日起郑州市施行《郑州市城市生活垃圾分类管理办法》,郑州将正式进入城市生活垃圾分类时代.为了增强社区居民对垃圾分类知识的了解,积极参与到垃圾分类的行动中,某社区采用线下和线上相结合的方式开展了一次200名辖区成员参加的“垃圾分类有关知识”专题培训.为了了解参训成员对于线上培训、线下培训的满意程度,社区居委会随机选取了40名辖区成员,将他们分成两组,每组20人,分别对线上、线下两种培训进行满意度测评,根据辖区成员的评分(满分100分)绘制了如图所示的茎叶图.
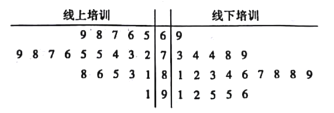
(1)根据茎叶图判断辖区成员对于线上、线下哪种培训的满意度更高,并说明理由.
(2)求这40名辖区成员满意度评分的中位数![]() ,并将评分不超过
,并将评分不超过![]() 、超过
、超过![]() 分别视为“基本满意”“非常满意”两个等级.
分别视为“基本满意”“非常满意”两个等级.
(ⅰ)利用样本估计总体的思想,估算本次培训共有多少辖区成员对线上培训非常满意;
(ⅱ)根据茎叶图填写下面的列联表.
基本满意 | 非常满意 | 总计 | |
线上培训 | |||
线下培训 | |||
总计 |
并根据列联表判断能否有99.5%的把握认为辖区成员对两种培训方式的满意度有差异?
附:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
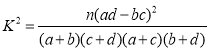 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在矩形ABCD中,AB=5,AD=2,点E在线段AB上,且BE=1,将△ADE沿DE折起到A1DE的位置,使得平面A1DE⊥平面BCDE.
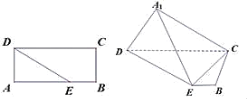
(1)求证:CE⊥平面A1DE;
(2)线段A1C上是否存在一点F,使得BF//平面A1DE?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
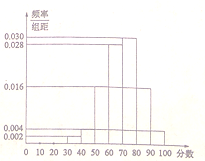
【题目】2016年某市政府出台了“2020年创建全国文明城市(简称创文)”的具体规划,今日,作为“创文”项目之一的“市区公交站点的重新布局及建设”基本完成,市有关部门准备对项目进行调查,并根据调查结果决定是否验收,调查人员分别在市区的各公交站点随机抽取若干市民对该项目进行评分,并将结果绘制成如图所示的频率分布直方图,相关规则为:①调查对象为本市市民,被调查者各自独立评分;②采用百分制评分, ![]() 内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
内认定为满意,80分及以上认定为非常满意;③市民对公交站点布局的满意率不低于60%即可进行验收;④用样本的频率代替概率.
(1)求被调查者满意或非常满意该项目的频率;
(2)若从该市的全体市民中随机抽取3人,试估计恰有2人非常满意该项目的概率;
(3)已知在评分低于60分的被调查者中,老年人占![]() ,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记
,现从评分低于60分的被调查者中按年龄分层抽取9人以便了解不满意的原因,并从中选取2人担任群众督察员,记![]() 为群众督查员中老年人的人数,求随机变量
为群众督查员中老年人的人数,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com