
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012学年浙江省杭州七校高一第二学期期中联考数学试卷(解析版) 题型:解答题
在 中,满足
中,满足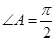 ,
,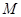 是
是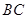 边上的一点.
边上的一点.
(Ⅰ)若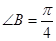 ,求向量
,求向量 与向量
与向量 夹角的正弦值;
夹角的正弦值;
(Ⅱ)若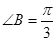 ,
, =m (m为正常数) 且
=m (m为正常数) 且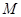 是
是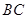 边上的三等分点.,求
边上的三等分点.,求 值;
值;
(Ⅲ)若 且
且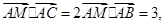 求
求 的最小值。
的最小值。
【解析】第一问中,利用向量的数量积设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则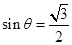 为所求
为所求
第二问因为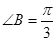 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则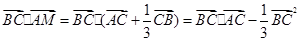 =
=
(2)当 时,则
时,则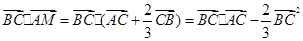 =
=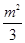
第三问中,解:设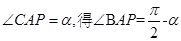 ,因为
,因为
 ,
, ;
;
所以 即
即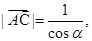 于是
于是 得
得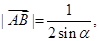
从而
运用三角函数求解。
(Ⅰ)解:设向量 与向量
与向量 的夹角为
的夹角为 ,则
,则
令 =
= ,得
,得 ,又
,又 ,则
,则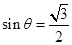 为所求……………2分
为所求……………2分
(Ⅱ)解:因为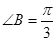 ,
, =m所以
=m所以 ,
,
(1)当 时,则
时,则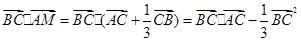 =
= ;-2分
;-2分
(2)当 时,则
时,则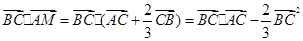 =
=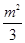 ;--2分
;--2分
(Ⅲ)解:设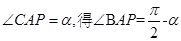 ,因为
,因为
 ,
, ;
;
所以 即
即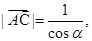 于是
于是 得
得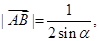
从而 ---2分
---2分
= =
=
= …………………………………2分
…………………………………2分
令 ,
,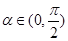 则
则 ,则函数
,则函数 ,在
,在 递减,在
递减,在 上递增,所以
上递增,所以 从而当
从而当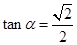 时,
时,
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题:①过离心率为e且焦点在x轴,中心在原点的双曲线的右焦点F的直线与双曲线右支交于A、B两点,弦AB的垂直平分线交x轴于P,则![]() ;②若函数
;②若函数![]() ,则f(x)是周期函数;③如图,二面角
,则f(x)是周期函数;③如图,二面角![]() 的大小是45°,线段
的大小是45°,线段![]() .
.![]() ,
,
![]() 与
与![]() 所成的角为30°.则
所成的角为30°.则![]() 与平面
与平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ;④三棱锥P—ABC的三条侧棱PA 、PB、PC两两垂直且长度均为1,四个顶点在同一个球面上,则A、B两点的球面距离是
;④三棱锥P—ABC的三条侧棱PA 、PB、PC两两垂直且长度均为1,四个顶点在同一个球面上,则A、B两点的球面距离是![]() ;其中正确的是 ;⑤已知
;其中正确的是 ;⑤已知![]() ,
,![]() ,且
,且![]() ,则
,则![]() 夹角的最大值是
夹角的最大值是![]() 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com