
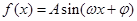 (其中
(其中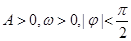 )的图象如下图所示。
)的图象如下图所示。 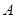 ,
,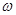 及
及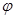 的值;
的值; 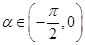 ,且
,且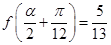 ,求
,求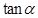 的值.。
的值.。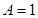 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。1分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。1分 ∵
∵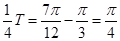 ∴
∴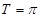 。。。。。。3分
。。。。。。3分 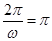 ∴
∴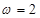 。。。。。。。。。。4分
。。。。。。。。。。4分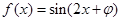
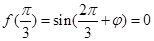 ,
,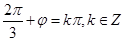 ∴
∴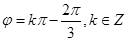 。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。6分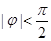 ,∴
,∴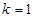 时,
时,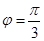 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分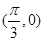 是五点作图的第三个点,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5分
是五点作图的第三个点,。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。5分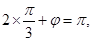 ∴
∴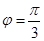 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分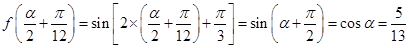 。。11分
。。11分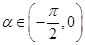 ∴
∴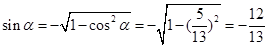 。。。。。。。。。。。13分
。。。。。。。。。。。13分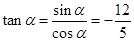 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。14分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。14分

 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:解答题
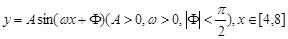 时的图象,图象的最高点为
时的图象,图象的最高点为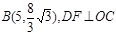 ,垂足为F。
,垂足为F。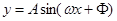 的解析式;
的解析式; 线OD上何处时,水上乐园的面积最大?
线OD上何处时,水上乐园的面积最大?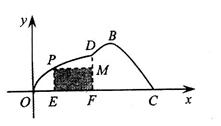
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
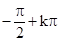 ,
,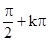 ),
),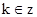 内都是增函数,不能说在整
内都是增函数,不能说在整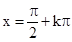 ,
,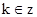
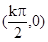 ,
,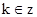
| A.3个 | B.4个 | C.5个 | D.6个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
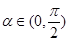 使
使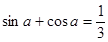 ②存在区间
②存在区间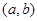 使
使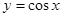 为减函数而
为减函数而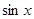 <0③
<0③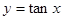 在其定义域内为增函数④
在其定义域内为增函数④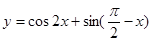 既有最大、最小值,又是偶函数⑤
既有最大、最小值,又是偶函数⑤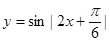 最小正周期为
最小正周期为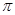 ,以上命题正确的为____________.
,以上命题正确的为____________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com