
����Ŀ��ij�������Ϊ�˽����Ƕ�ij����Ʒ��ʹ������Ƿ����Ա��йأ������Ͻ������ʾ����飬�ڵ������������ȡ��![]() �ݽ���ͳ�ƣ��õ�����
�ݽ���ͳ�ƣ��õ�����![]() ��������
��������
���� | Ů�� | �ϼ� | |
ʹ�� | 15 | 5 | 20 |
��ʹ�� | 10 | 20 | 30 |
�ϼ� | 25 | 25 | 50 |
��1������ݵ��������ж�������Ϊʹ�øò�Ʒ���Ա��йأ�
��2���ڲ�ʹ�øò�Ʒ�����У����Ա��÷ֲ������ȡ![]() �ˣ��ٴ���
�ˣ��ٴ���![]() ���������ȡ
���������ȡ![]() �˲μ�ij�����DZ����вμӸ�����Ů������Ϊ
�˲μ�ij�����DZ����вμӸ�����Ů������Ϊ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
����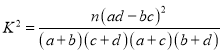 ��
��
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
���𰸡���1����![]() ������Ϊʹ�øò�Ʒ���Ա��йأ�2���������
������Ϊʹ�øò�Ʒ���Ա��йأ�2���������
��������
��1�����������ݣ�����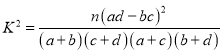 �õ�
�õ�![]() �Ĺ۲�ֵ�������ٽ�ֵ�������ɵó������
�Ĺ۲�ֵ�������ٽ�ֵ�������ɵó������
��2�������⣬���ݷֲ�����ķ����õ���ȡ![]() ��������Ӧ��ȡ
��������Ӧ��ȡ![]() �ˣ�Ů��Ӧ��ȡ
�ˣ�Ů��Ӧ��ȡ![]() �ˣ��ٴ��������ȡ
�ˣ��ٴ��������ȡ![]() �˲μ�ij������Ů��������Ϊ
�˲μ�ij������Ů��������Ϊ![]() ��������ȷ��
��������ȷ��![]() �����п���ȡֵ�������Ӧ�ĸ��ʣ������ɵó��ֲ��У��������.
�����п���ȡֵ�������Ӧ�ĸ��ʣ������ɵó��ֲ��У��������.
��1�����������ݿɵ�,
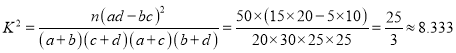 ��
��
����![]() ��������
��������![]() ������Ϊʹ�øò�Ʒ���Ա��йأ�
������Ϊʹ�øò�Ʒ���Ա��йأ�
��2����![]() ������֪����ʹ�øò�Ʒ������Ϊ
������֪����ʹ�øò�Ʒ������Ϊ![]() ����������
����������![]() �ˣ�Ů��
�ˣ�Ů��![]() �ˣ����Ա��÷ֲ������ȡ
�ˣ����Ա��÷ֲ������ȡ![]() ��������Ӧ��ȡ
��������Ӧ��ȡ![]() �ˣ�Ů��Ӧ��ȡ
�ˣ�Ů��Ӧ��ȡ![]() �ˣ��ٴ��������ȡ
�ˣ��ٴ��������ȡ![]() �˲μ�ij������Ů��������Ϊ
�˲μ�ij������Ů��������Ϊ![]() ����
����![]() �����п���ȡֵΪ��
�����п���ȡֵΪ��![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��![]() ��
��
����![]() �ĸ��ʷֲ���Ϊ
�ĸ��ʷֲ���Ϊ
|
|
|
|
|
|
|
|
��ѧ����Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������![]() ���������ȥ������һ��Ԫ��
���������ȥ������һ��Ԫ��![]() ֮��ʣ�������Ԫ����ɵļ��϶��ܷ�Ϊ��������Ϊ�ռ��ļ��ϣ������������ϵ�����Ԫ��֮����ȣ��ͳƼ���
֮��ʣ�������Ԫ����ɵļ��϶��ܷ�Ϊ��������Ϊ�ռ��ļ��ϣ������������ϵ�����Ԫ��֮����ȣ��ͳƼ���![]() Ϊ���ɷּ��ϡ�.
Ϊ���ɷּ��ϡ�.
��1���жϼ���![]() ��
��![]() �Ƿ��ǡ��ɷּ��ϡ�������д���̣���
�Ƿ��ǡ��ɷּ��ϡ�������д���̣���
��2����֤�����Ԫ�صļ���![]() һ�����ǡ��ɷּ��ϡ���
һ�����ǡ��ɷּ��ϡ���
��3��������![]() �ǡ��ɷּ��ϡ�.
�ǡ��ɷּ��ϡ�.
��֤����![]() Ϊ������
������
����![]() ��Ԫ�ظ�������Сֵ.
��Ԫ�ظ�������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]()
��1����![]() ʱ����ʽ
ʱ����ʽ![]() �Ľ⼯��
�Ľ⼯��
��2��������ʽ![]() �Ľ⼯Ϊ�ռ�����ʵ��
�Ľ⼯Ϊ�ռ�����ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������й�����70��������ı�����У��ڶ�Ⱥ������������һ�ź��ģ��Դ˱����������Ȱ�֮�飬����ѧ�У��ж��ַ��̶����Ա�ʾ�������ߣ������������ĵѿ����������ߣ���ͼ����ֱ������ϵ�У���ԭ��OΪ���㣬x��������Ϊ���Ὠ��������ϵ.ͼ�е����߾��ǵѿ����������ߣ��伫���귽��Ϊ![]() ��
��![]() ����MΪ�������ϵ�����һ��.
����MΪ�������ϵ�����һ��.

��1����![]() ʱ����M��ļ����ꣻ
ʱ����M��ļ����ꣻ
��2��������OM��ԭ��O��ʱ����ת![]() ��������ཻ�ڵ�N����
��������ཻ�ڵ�N����![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ʱ������
ʱ������![]() �ĵ����ԣ�
�ĵ����ԣ�
��2����![]() ��������
��������![]() �IJ���ʽ
�IJ���ʽ![]() ��
��![]() ���н⣬��
���н⣬��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���������������ŵij�Ա�У��ֱ��и�һ���߶��������꼶��1��2��3�������������ѵ�ѧ�����ڸ�У��Ԫ����Ŀ�������У�Ҫ����6��ѧ����ѡȡ���˵��ν�Ŀ�����ˣ���������һ���Ǹ���ѧ���ĸ�����_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ![]() ��tΪ����������OΪ���㣬x��������Ϊ���Ὠ��������ϵ������C�ļ����귽��Ϊ��������2sin������1��
��tΪ����������OΪ���㣬x��������Ϊ���Ὠ��������ϵ������C�ļ����귽��Ϊ��������2sin������1��
��1����C��ֱ�����귽�̣�
��2����ֱ��l��y���ཻ��P��������C�ཻ��A��B���㣬��|PA|+|PB|��2�����O��ֱ��l�ľ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�ֱ��l�IJ�������Ϊ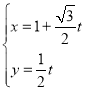 ��tΪ������������OΪ���㣬x��������Ϊ����ļ�����ϵ�У�����C�ļ����귽��Ϊ��sin2����4cos����
��tΪ������������OΪ���㣬x��������Ϊ����ļ�����ϵ�У�����C�ļ����귽��Ϊ��sin2����4cos����
��1����ֱ��l����ͨ����������C��ֱ�����귽�̣�
��2����ֱ��l��x��Ľ���ΪF��ֱ��l������C�Ľ���ΪA��B����|FA|+|FB|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��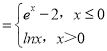 ��g��x����f��
��g��x����f��![]() ��+1��k��R��k��0���������й��ں���y��f[g��x��]+1���������ж���ȷ���ǣ� ��
��+1��k��R��k��0���������й��ں���y��f[g��x��]+1���������ж���ȷ���ǣ� ��
A.��k��0ʱ����2����㣻��k��0ʱ����4�����
B.��k��0ʱ����4����㣻��k��0ʱ����2�����
C.����kΪ��ֵ������2�����
D.����kΪ��ֵ������4�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com