
【题目】已知函数f(x)=sin2x+sinx+cosx,以下说法中不正确的是( )
A.f(x)周期为2π
B.f(x)最小值为﹣ ![]()
C.f(x)在区间[0, ![]() ]单调递增
]单调递增
D.f(x)关于点x= ![]() 对称
对称
【答案】C
【解析】解:①∵f(x+2π)=sin[2(x+2π)]+sin(x+2π)+cos(x+2π)=sin2x+sinx+cosx=f(x),
∴函数周期为2π,故①正确;
②设t=sinx+cosx= ![]() sin(x+
sin(x+ ![]() )∈[﹣
)∈[﹣ ![]() ,
, ![]() ],
],
∴t2=(sinx+cosx)2=1+sin2x,
∴sin2x=t2﹣1,
∴y=sin2x+sinx+cosx=t2﹣1+t=t2+t﹣1=(t+ ![]() )2﹣
)2﹣ ![]() ,t∈[﹣
,t∈[﹣ ![]() ,
, ![]() ],
],
由二次函数可知,当t∈[﹣ ![]() ,﹣
,﹣ ![]() ]时,函数y=t2+t﹣1单调递减,当t∈[﹣
]时,函数y=t2+t﹣1单调递减,当t∈[﹣ ![]() ,
, ![]() ]时,函数y=t2+t﹣1单调递增,
]时,函数y=t2+t﹣1单调递增,
∴当t=﹣ ![]() 时,函数取最小值ymin=﹣
时,函数取最小值ymin=﹣ ![]() ,故②正确;
,故②正确;
③∵f(x)=sin2x+sinx+cosx,
当x= ![]() 时,f(x)=1+
时,f(x)=1+ ![]() ,
,
当x= ![]() 时,f(x)=1,
时,f(x)=1,
∴f(x)在区间[0, ![]() ]不是单调递增.
]不是单调递增.
故③错误;
④∵f( ![]() ﹣x)=sin[2(
﹣x)=sin[2( ![]() ﹣x)]+sin(
﹣x)]+sin( ![]() ﹣x)+cos(
﹣x)+cos( ![]() ﹣x)=sin(π﹣2x)+sinx+cosx=sin2x+sinx+cosx=f(x),
﹣x)=sin(π﹣2x)+sinx+cosx=sin2x+sinx+cosx=f(x),
∴函数关于x= ![]() 对称,故④正确.
对称,故④正确.
所以答案是:C.


科目:高中数学 来源: 题型:
【题目】在一次商贸交易会上,商家在柜台开展促销抽奖活动,甲、乙两人相约同一天上午去该柜台参与抽奖.
(1)若抽奖规则是从一个装有![]() 个红球和
个红球和 ![]() 个白球的袋中一次取出
个白球的袋中一次取出![]() 个球,当两个球同色时则中奖,求中奖概率;
个球,当两个球同色时则中奖,求中奖概率;
(2)若甲计划在![]() 之间赶到,乙计划在
之间赶到,乙计划在![]() 之间赶到,求甲比乙提前到达的概率.
之间赶到,求甲比乙提前到达的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为![]() .
.
(1)求椭圆![]() 的方程式;
的方程式;
(2)已知动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
①若线段![]() 中点的横坐标为
中点的横坐标为![]() ,求斜率
,求斜率![]() 的值;
的值;
②已知点![]() ,求证:
,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设满足以下两个条件的有穷数列![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 阶“期待数列”:
阶“期待数列”:
①![]() ;
;
②![]() .
.
(![]() )分别写出一个单调递增的
)分别写出一个单调递增的![]() 阶和
阶和![]() 阶“期待数列”.
阶“期待数列”.
(![]() )若某
)若某![]() 阶“期待数列”是等差数列,求该数列的通项公式.
阶“期待数列”是等差数列,求该数列的通项公式.
(![]() )记
)记![]() 阶“期待数列”的前
阶“期待数列”的前![]() 项和为
项和为![]() ,试证:
,试证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.

(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆C: ![]() =1(a>b>0)过点P(1,
=1(a>b>0)过点P(1, ![]() ).离心率为
).离心率为![]() .
.
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A,B两点.
①若直线l过椭圆C的右焦点,记△ABP三条边所在直线的斜率的乘积为t.
求t的最大值;
②若直线l的斜率为![]() ,试探究OA2+ OB2是否为定值,若是定值,则求出此
,试探究OA2+ OB2是否为定值,若是定值,则求出此
定值;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
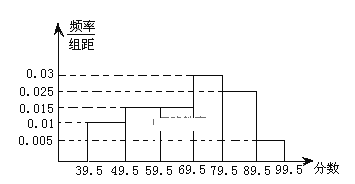
【题目】如图,从参加环保知识竞赛的学生中抽出![]() 名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:
(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(![]() 分及以上为及格)和平均数?
分及以上为及格)和平均数?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级进行了一次学业水平测试,用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究.经统计,成绩的分组及各组的频数如下: ![]() ,2;
,2; ![]() ,3;
,3; ![]() ,10;
,10; ![]()
15; ![]() ,12;
,12; ![]() ,8.
,8.
(1)完成样本的频率分布表,画出频率分布直方图;
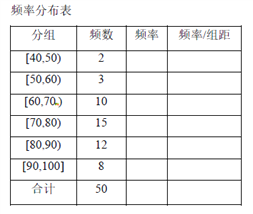
(2)估计成绩在85分以下的学生比例;
(3)请你根据以上信息去估计样本的众数、中位数、平均数(精确到0.01).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com