
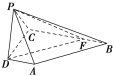
【题目】如图,在四棱锥PABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.

(1)求异面直线AP与BC所成角的余弦值;
(2)求证:PD⊥平面PBC;
(3)求直线AB与平面PBC所成角的正弦值.
【答案】(1)![]() (2)见解析(3)
(2)见解析(3)![]()
【解析】
(Ⅰ)由已知AD∥BC,从而∠DAP或其补角即为异面直线AP与BC所成的角,由此能求出异面直线AP与BC所成角的余弦值.
(Ⅱ)由AD⊥平面PDC,得AD⊥PD,由BC∥AD,得PD⊥BC,再由PD⊥PB,得到PD⊥平面PBC.
(Ⅲ)过点D作AB的平行线交BC于点F,连结PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角,由PD⊥平面PBC,得到∠DFP为直线DF和平面PBC所成的角,由此能求出直线AB与平面PBC所成角的正弦值.
(1)如图,由已知AD∥BC,故∠DAP或其补角即为异面直线AP与BC所成的角.
因为AD⊥平面PDC,直线PD平面PDC,所以AD⊥PD.
在Rt△PDA中,由已知,得AP=![]() ,
,
故cos∠DAP=![]() =
=![]() .
.
所以,异面直线AP与BC所成角的余弦值为![]() .
.
(2)证明:由(1)知AD⊥PD.又因为BC∥AD,所以PD⊥BC.又PD⊥PB,PB∩BC=B,所以PD⊥平面PBC.
(3)解:过点D作DF∥AB,交BC于点F,连接PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.
因为PD⊥平面PBC,所以PF为DF在平面PBC上的射影,
所以∠DFP为直线DF和平面PBC所成的角.
由于AD∥BC,DF∥AB,故BF=AD=1.
由已知,得CF=BC-BF=2.
又AD⊥DC,所以BC⊥DC.
在Rt△DCF中,可得DF=2![]() ,
,
在Rt△DPF中,可得sin∠DFP=![]() .
.
所以直线AB与平面PBC所成角的正弦值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设有关于x 的一元二次方程![]()
(1)若![]() 是从0,1,2,3,4五个数中任取的一个数,
是从0,1,2,3,4五个数中任取的一个数,![]() 是从0,1,2,3四个数中任取的一个数,求上述方程有实数根的概率;
是从0,1,2,3四个数中任取的一个数,求上述方程有实数根的概率;
(2)若![]() 是从区间
是从区间![]() 中任取的一个实数,
中任取的一个实数,![]() 是从区间
是从区间![]() 中任取的一个实数,求上述方程有实数根的概率.
中任取的一个实数,求上述方程有实数根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() ,且
,且![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() ,
,![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)求证:![]() 平面
平面![]() .
.
(Ⅲ)写出四棱锥![]() 的体积.(只写出结论,不需要说明理由)
的体积.(只写出结论,不需要说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() 分别为双曲线
分别为双曲线![]() 的左、右焦点,
的左、右焦点, ![]() 为双曲线的左顶点,以
为双曲线的左顶点,以![]() ,
, ![]() 为直径的圆交双曲线某条渐近线于
为直径的圆交双曲线某条渐近线于![]() ,
, ![]() 两点,且满足
两点,且满足![]() ,则该双曲线的离心率为________.
,则该双曲线的离心率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设内角A、B、C的对边分别为a、b、c,向量 ![]() =(cosA+
=(cosA+ ![]() ,sinA),向量
,sinA),向量 ![]() =(﹣sinA,cosA),若|
=(﹣sinA,cosA),若| ![]() +
+ ![]() |=2.
|=2.
(1)求角A的大小;
(2)若b=4 ![]() ,且c=
,且c= ![]() a,求△ABC的面积.
a,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]()
(1)若![]() 且函数
且函数![]() 的值域为
的值域为![]() ,求
,求![]() 的表达式;
的表达式;
(2)在(1)的条件下, 当![]() 时,
时, ![]() 是单调函数, 求实数k的取值范围;
是单调函数, 求实数k的取值范围;
(3)设![]() ,
, ![]()
![]() 且
且![]() 为偶函数, 判断
为偶函数, 判断![]() +
+![]() 能否大于零?请说明理由.
能否大于零?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合P={(x,y)||x|+|y|≤1,x∈R,y∈R},Q={(x,y)|x2+y2≤1,x∈R,y∈R},R={(x,y)|x4+y2≤1,x∈R,y∈R}则下列判断正确的是( )
A.PQR
B.PRQ
C.QPR
D.RPQ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如图2,连结
,如图2,连结![]() ,
, ![]() .
.
(Ⅰ)求证:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 为
为![]() 中点,求直线
中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com