
【题目】A市积极倡导学生参与绿色环保活动,其中代号为“环保卫士——12369”的绿色环保活动小组对2014年1月——2014年12月(一年)内空气质量指数![]() 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若A市某企业每天由空气污染造成的经济损失P(单位:元)与空气质量指数![]() (记为t)的关系
(记为t)的关系
为: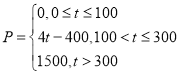 ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,完成![]() 列联表,并判断是
列联表,并判断是
否有![]() 的把握认为A市本年度空气重度污染与供暖有关?
的把握认为A市本年度空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季节 | |||
合计 | 100 |
下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | p>5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
【答案】(1)P(A)=![]() ;(2)95%的把握认为A市本年度空气重度污染与供暖有关.
;(2)95%的把握认为A市本年度空气重度污染与供暖有关.
【解析】
试题分析:本题第一问经济损失![]() 元,只可能是第二段函数在此范围类,从而得到t的范围,进而通过频数统计表得到所对应的天数,利用古典概型概率公式得其概率.第二问列联表的完成只要找到各个数据所对应的含义不难完成,然后利用独立性检验相关系数看相关性大小,注意从表中查到的是出错的概率.
元,只可能是第二段函数在此范围类,从而得到t的范围,进而通过频数统计表得到所对应的天数,利用古典概型概率公式得其概率.第二问列联表的完成只要找到各个数据所对应的含义不难完成,然后利用独立性检验相关系数看相关性大小,注意从表中查到的是出错的概率.
试题解析:(1)设“在本年内随机抽取一天,该天经济损失P∈(200,600]元”为事件A
由200<4t﹣400≤600,得150<t≤250,频数为39,
∴P(A)=![]()
(2)根据以上数据得到如表:
非重度污染 | 重度污染 | 合计 | |
供暖季 | 22 | 8 | 30 |
非供暖季 | 63 | 7 | 70 |
合计 | 85 | 15 | 100 |
K2的观测值K2=![]() ≈4.575>3.841
≈4.575>3.841
所以有95%的把握认为A市本年度空气重度污染与供暖有关.


科目:高中数学 来源: 题型:
【题目】某大学专业有数学分析、解析几何、高等代数三个科目的选修课,甲、乙两位同学各随机选择两科,则数学分析至少被一位同学选中的概率为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为支援武汉抗击疫情,某医院准备从6名医生和3名护士中选出5人组成一个医疗小组远赴武汉,请解答下列问题:(用数字作答)
(1)如果这个医疗小组中医生和护士都不能少于2人,共有多少种不同的建组方案?
(2)医生甲要担任医疗小组组长,所以必选,而且医疗小组必须医生和护士都有,共有多少种不同的建组方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,M为PA上一点,且
,M为PA上一点,且![]() ,
,
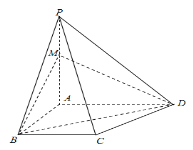
(1)证明:PC//平面MBD;
(2)若![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求直线AB与平面MBD所成角的正弦值.
,求直线AB与平面MBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为支援边远地区教育事业的发展,现有5名师范大学毕业生主动要求赴西部某地区三所不同的学校去支教,每个学校至少去1人,甲、乙不能安排在同一所学校,则不同的安排方法有( )
A.180种B.150种C.90种D.114种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com