
【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为 ![]()

(1)求频率分布图中 ![]() 的值,并估计该企业的职工对该部门评分不低于80的概率;
的值,并估计该企业的职工对该部门评分不低于80的概率;
(2)从评分在 ![]() 的受访职工中,随机抽取2人,求此2人评分都在
的受访职工中,随机抽取2人,求此2人评分都在 ![]() 的概率.
的概率.
科目:高中数学 来源: 题型:
【题目】某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45)岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
A.31.6岁
B.32.6岁
C.33.6岁
D.36.6岁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.经过点P0(x0 , y0)的直线都可以用方程y-y0=k(x-x0)表示
B.经过定点A(0,b)的直线都可以用方程y=kx+b表示
C.经过任意两个不同点P1(x1 , y1),P2(x2 , y2)的直线都可用方程(x2-x1)(y-y1)=(y2-y1)(x-x1)表示
D.不经过原点的直线都可以用方程 ![]() 表示
表示
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, ![]() 是圆柱的母线,
是圆柱的母线, ![]() 是
是 ![]() 的直径,
的直径, ![]() 是底面圆周上异于
是底面圆周上异于 ![]() 的任意一点,
的任意一点, ![]() ,
, ![]() .
.
(1)求证: ![]()
(2)当三棱锥 ![]() 的体积最大时,求
的体积最大时,求 ![]() 与平面
与平面 ![]() 所成角的大小;
所成角的大小;
(3)![]() 上是否存在一点
上是否存在一点 ![]() ,使二面角
,使二面角 ![]() 的平面角为45°?若存在,求出此时
的平面角为45°?若存在,求出此时 ![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3﹣ax2+(a2﹣1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y﹣3=0.
x3﹣ax2+(a2﹣1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y﹣3=0.
(1)求a,b的值;
(2)求函数f(x)的单调区间,并求出f(x)在区间[﹣2,4]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点.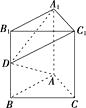
求证:AD⊥平面A1DC1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com