
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数,
为参数,![]() ).
).
(Ⅰ)当![]() 时,若曲线
时,若曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,求直线
成中心对称,求直线![]() 的参数方程;
的参数方程;
(Ⅱ)在以原点为极点,![]() 轴的正半轴为极轴的极坐标系中,极坐标方程为
轴的正半轴为极轴的极坐标系中,极坐标方程为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为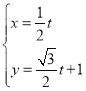 (
(![]() 为参数),曲线
为参数),曲线![]() 的普通方程为
的普通方程为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(I)求直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(II)设点D在曲线![]() 上,且曲线
上,且曲线![]() 在点D处的切线与直线
在点D处的切线与直线![]() 垂直,试确定点D的坐标.
垂直,试确定点D的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】原命题:“![]() ,
,![]() 为两个实数,若
为两个实数,若![]() ,则
,则![]() ,
,![]() 中至少有一个不小于1”,下列说法错误的是
中至少有一个不小于1”,下列说法错误的是
A.逆命题为:若![]() ,
,![]() 中至少有一个不小于1则
中至少有一个不小于1则![]() ,为假命题
,为假命题
B.否命题为:若![]() 则
则![]() ,
,![]() 都小于1 ,为假命题
都小于1 ,为假命题
C.逆否命题为:若![]() ,
,![]() 都小于1则
都小于1则![]() ,为真命题
,为真命题
D.“![]() ”是“
”是“![]() ,
,![]() 中至少有一个不小于1”的必要不充分条件
中至少有一个不小于1”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意实数x,不等式ax2+2ax﹣(a+2)<0恒成立,则实数a的取值范围是( )
A.﹣1≤a≤0
B.﹣1≤a<0
C.﹣1<a≤0
D.﹣1<a<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某消防机构为![]() 四个小区的居民代表进行消防安全知识宣传.在代表中,按分层抽样的方式抽取了10名“幸运之星”,“幸运之星”每人获得一份纪念品.相关数据如下:
四个小区的居民代表进行消防安全知识宣传.在代表中,按分层抽样的方式抽取了10名“幸运之星”,“幸运之星”每人获得一份纪念品.相关数据如下:
小区 | A | B | C | D |
代表人数 | 45 | 60 | 30 | 15 |
(I)求此活动中各小区“幸运之星”的人数;
(II)从B小区和C小区的“幸运之星”中任选两人进行后续的活动,求这两个人均来自B小区的概率;
(III)消防机构在B小区内,对参加问答活动的居民进行了是否有兴趣参加消防安全培训的问卷调查,统计结果如下(单位:人):
有兴趣 | 无兴趣 | 合计 | |
男 | 25 | 5 | 30 |
女 | 15 | 15 | 30 |
合计 | 40 | 20 | 60 |
据此判断能否在犯错误的概率不超过![]() 的前提下认为有兴趣参加消防安全培训与性别有关系?
的前提下认为有兴趣参加消防安全培训与性别有关系?
临界值表:
|
|
|
|
|
|
|
|
|
|
参考公式: ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】二手车经销商小王对其所经营的![]() 型号二手汽车的使用年数
型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下数据:
(单位:万元/辆)进行整理,得到如下数据:
使用年数 | 2 | 3 | 4 | 5 | 6 | 7 |
售价 | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
下面是![]() 关于
关于![]() 的散点图:
的散点图:

(I)由散点图看出,可以用线性回归模型拟合![]() 和
和![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(II)求![]() 关于
关于![]() 的回归方程,并预测某辆
的回归方程,并预测某辆![]() 型号二手汽车当使用年数为9年时,售价大约为多少?(
型号二手汽车当使用年数为9年时,售价大约为多少?(![]() 、
、![]() 的值精确到
的值精确到![]() )
)
(III)基于成本的考虑,该型号二手汽车的售价不得低于7118元,请根据(II)求出的回归方程预测在收购该型号二手汽车时,车辆的使用年数不得超过多少年?
参考公式: ,相关系数
,相关系数 .
.
参考数据:![]() ,
, ,
, ,
, ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新生儿Apgar评分,即阿氏评分是对新生儿出生后总体状况的一个评估,主要从呼吸、心率、反射、肤色、肌张力这几个方面评分,满10分者为正常新生儿,评分7分以下的新生儿考虑患有轻度窒息,评分在4分以下考虑患有重度窒息,大部分新生儿的评分多在7-10分之间,某市级医院妇产科对1月份出生的新生儿随机抽取了16名,以下表格记录了他们的评分情况.
(1)现从16名新生儿中随机抽取3名,求至多有1名评分不低于9分的概率;
(2)以这16名新生儿数据来估计本年度的总体数据,若从本市本年度新生儿任选3名,记![]() 表示抽到评分不低于9分的新生儿数,求
表示抽到评分不低于9分的新生儿数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com