
【题目】如图,某观测站在港口A的南偏西40°方向的C处,测得一船在距观测站31海里的B处,正沿着从港口出发的一条南偏东20°的航线上向港口A开去,当船走了20海里到达D处,此时观测站又测得CD等于21海里,问此时船离港口A处还有多远? 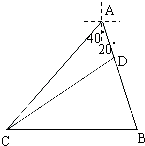
科目:高中数学 来源: 题型:
【题目】在△ABC中,tanA是以﹣4为第三项,4为第七项的等差数列的公差,tanB是以2为公差,9为第五项的等差数列的第二项,则这个三角形是( )
A.锐角三角形
B.钝角三角形
C.等腰直角三角形
D.等腰或直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一房产商竞标得一块扇形OPQ地皮,其圆心角∠POQ= ![]() ,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议.
,半径为R=200m,房产商欲在此地皮上修建一栋平面图为矩形的商住楼,为使得地皮的使用率最大,准备了两种设计方案如图,方案一:矩形ABCD的一边AB在半径OP上,C在圆弧上,D在半径OQ;方案二:矩形EFGH的顶点在圆弧上,顶点G,H分别在两条半径上.请你通过计算,为房产商提供决策建议. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=asin2x+bcos2x(ab≠0),有下列四个命题:其中正确命题的序号为(填上所有正确命题的序号)
①若a=1,b=﹣ ![]() ,要得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移
,要得到函数y=f(x)的图象,只需将函数y=2sin2x的图象向右平移 ![]() 个单位;
个单位;
②若a=1,b=﹣1,则函数y=f(x)的一个对称中心为( ![]() ,0);
,0);
③若y=f(x)的一条对称轴方程为x= ![]() ,则a=b;
,则a=b;
④若方程asin2x+bcos2x=m的正实数根从小到大依次构成一个等差数列,则这个等差数列的公差为π.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 关于直线
关于直线![]() 对称的圆为
对称的圆为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() 两点,
两点, ![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() 中
中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 分别到两定点
分别到两定点![]()
![]() 连线的斜率之乘积为
连线的斜率之乘积为![]() ,设
,设![]() 的轨迹为曲线
的轨迹为曲线![]() ,
, ![]() ,
, ![]() 分别为曲线
分别为曲线![]() 的左右焦点,则下列命题中:
的左右焦点,则下列命题中:
(1)曲线![]() 的焦点坐标为
的焦点坐标为![]() ,
, ![]() ;
;
(2)若![]() ,则
,则![]()
![]() ;
;
(3)当![]() 时,
时, ![]() 的内切圆圆心在直线
的内切圆圆心在直线![]() 上;
上;
(4)设![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高二年级学生中随机抽取了20名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图.

![]() 求图中实数a的值;
求图中实数a的值;
![]() 若该校高二年级共有学生600名,试估计该校高二年级期中考试数学成绩不低于60分的人数;
若该校高二年级共有学生600名,试估计该校高二年级期中考试数学成绩不低于60分的人数;
![]() 若从数学成绩在[60,70)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值大于10的概率.
若从数学成绩在[60,70)与[90,100]两个分数段内的学生中随机选取2名学生,求这2名学生的数学成绩之差的绝对值大于10的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中, ![]() 是等腰直角三角形,
是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,
, ![]() 分别为
分别为![]() 与
与![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 上的射影是
上的射影是![]() 的重心.
的重心.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com