
【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况,![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
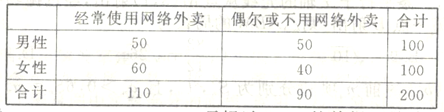
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

【答案】(1)不能在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖情况与性别有关.
市使用网络外卖情况与性别有关.
(2)①![]() ;②
;②![]() ;
;![]() .
.
【解析】试题分析:(1)计算![]() 的值,进而可查表下结论;
的值,进而可查表下结论;
(2)①由分层抽样的抽样比计算即可;
②由![]() 列联表,可知抽到经常使用网络外卖的网民的频率为
列联表,可知抽到经常使用网络外卖的网民的频率为![]() ,将频率视为概率,即从
,将频率视为概率,即从![]() 市市民中任意抽取1人,恰好抽到经常使用网络外卖的市民的概率为
市市民中任意抽取1人,恰好抽到经常使用网络外卖的市民的概率为![]() ,由题意得
,由题意得![]() .
.
试题解析:
(1)由列联表可知![]() 的观测值,
的观测值,![]()
![]() .
.
所以不能在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖情况与性别有关.
市使用网络外卖情况与性别有关.
(2)①依题意,可知所抽取的5名女网民中,经常使用网络外卖的有![]() (人),
(人),
偶尔或不用网络外卖的有![]() (人).
(人).
则选出的3人中至少有2人经常使用网络外卖的概率为![]() .
.
②由![]() 列联表,可知抽到经常使用网络外卖的网民的频率为
列联表,可知抽到经常使用网络外卖的网民的频率为![]() ,
,
将频率视为概率,即从![]() 市市民中任意抽取1人,
市市民中任意抽取1人,
恰好抽到经常使用网络外卖的市民的概率为![]() .
.
由题意得![]() ,
,
所以![]() ;
;
![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定理:“实数m,n为常数,若函数h(x)满足h(m+x)+h(m﹣x)=2n,则函数y=h(x)的图象关于点(m,n)成中心对称”.
(1)已知函数f(x)= ![]() 的图象关于点(1,b)成中心对称,求实数b的值;
的图象关于点(1,b)成中心对称,求实数b的值;
(2)已知函数g(x)满足g(2+x)+g(﹣x)=4,当x∈[0,2]时,都有g(x)≤3成立,且当x∈[0,1]时,g(x)=2k(x﹣1)+1 , 求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△OAB中,点P为线段AB上的一个动点(不包含端点),且满足 ![]() =λ
=λ ![]() .
. 
(1)若λ= ![]() ,用向量
,用向量 ![]() ,
, ![]() 表示
表示 ![]() ;
;
(2)若| ![]() |=4,|
|=4,| ![]() |=3,且∠AOB=60°,求
|=3,且∠AOB=60°,求 ![]()
![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有老、中、青职工430人,其中青年职工160人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工32人,则该样本中的老年职工人数为( )
A.9
B.18
C.27
D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:y=ax+1﹣a(a∈R).若存在实数a使得一条曲线与直线l有两个不同的交点,且以这两个交点为端点的线段长度恰好等于|a|,则称此曲线为直线l的“绝对曲线”.下面给出四条曲线方程:①y=﹣2|x﹣1|;②y=x2;③(x﹣1)2+(y﹣1)2=1;④x2+3y2=4;则其中直线l的“绝对曲线”有( )
A.①④
B.②③
C.②④
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间![]() ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com