
【题目】如图所示的几何体中,四边形![]() 为等腰梯形,
为等腰梯形, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为正方形,平面
为正方形,平面![]() 平面
平面![]() .
.

(1)若点![]() 是棱
是棱![]() 的中点,求证:
的中点,求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)要证线面平行,一般先证线线平行,由![]() 是
是![]() 中点及其他已知可证
中点及其他已知可证![]() 与
与![]() 平行且相等,从而得平行四边形
平行且相等,从而得平行四边形![]() ,也就有线线平行
,也就有线线平行![]() ,从而得线面平行;
,从而得线面平行;
(2)由已知证得![]() 两两垂直,以它们为坐标轴建立空间直角坐标系,写出相应点的坐标,求出平行
两两垂直,以它们为坐标轴建立空间直角坐标系,写出相应点的坐标,求出平行![]() 的法向量,由直线的方向向量与平面法向量夹角余弦的绝对值等于直线与平面所成角的正弦值可得结论.
的法向量,由直线的方向向量与平面法向量夹角余弦的绝对值等于直线与平面所成角的正弦值可得结论.
试题解析:
(1)证明:由已知得![]() //
// ![]() ,且
,且![]() .
.
因为![]() 为等腰梯形,所以有
为等腰梯形,所以有![]() //
// ![]() .
.
因为![]() 是棱
是棱![]() 的中点,所以
的中点,所以![]() .
.
所以![]() //
// ![]() ,且
,且![]() ,
,
故四边形![]() 为平行四边形,
为平行四边形,
所以![]() //
// ![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]() .
.
解:(2)因为四边形![]() 为正方形,所以
为正方形,所以![]() .
.
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
在△![]() 中,因为
中,因为![]() ,
, ![]() ,
,
所以由余弦定理,得![]() ,
,
所以![]() .
.
在等腰梯形![]() 中,可得
中,可得![]() .
.
如图,以![]() 为原点,以
为原点,以![]() 所在直线分别为
所在直线分别为
![]() 轴, 建立空间坐标系,
轴, 建立空间坐标系,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,  ,
,
所以![]() ,
,  ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,由
,由
所以 ,取
,取![]() ,则
,则![]() ,得
,得![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则
![]()
所以![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】已知直线![]() :
: ![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
, ![]() 两点,记抛物线在
两点,记抛物线在![]() ,
, ![]() 两点处的切线
两点处的切线![]() ,
, ![]() 的交点为
的交点为![]() .
.
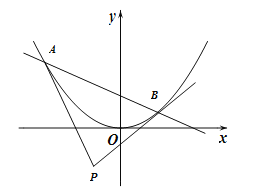
(I)求证: ![]() ;
;
(II)求点![]() 的坐标(用
的坐标(用![]() ,
, ![]() 表示);
表示);
(Ⅲ)若![]() ,求△
,求△![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将号码分别为1、2、…、9的九个小球放入一个袋中,这些小球仅号码不同,其余完全相同,甲从袋中摸出一个球.其号码为a,放回后,乙从此袋中再摸出一个球,其号码为b,则使不等式a-2b+10>0成立的事件发生的概率等于________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)= ![]() 若a,b,c,d各不相同,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围是( )
若a,b,c,d各不相同,且f(a)=f(b)=f(c)=f(d),则abcd的取值范围是( )
A.(24,25)
B.[16,25)
C.(1,25)
D.(0,25]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1= ![]() ,an+1an=2an+1﹣1(n∈N*),令bn=an﹣1.
,an+1an=2an+1﹣1(n∈N*),令bn=an﹣1.
(1)求数列{bn}的通项公式;
(2)令cn= ![]() ,求证:c1+c2+…+cn<n+
,求证:c1+c2+…+cn<n+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若a和b是计算机在区间(0,2)上产生的均匀随机数,则一元二次不等式ax2+4x+4b>0(a>0)的解集不是R的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]()
(1)讨论![]() 的单调区间和极值;
的单调区间和极值;
(2)将函数![]() 的图象向下平移1个单位后得到
的图象向下平移1个单位后得到![]() 的图象,且
的图象,且![]() 为自然对数的底数)和
为自然对数的底数)和![]() 是函数
是函数![]() 的两个不同的零点,求
的两个不同的零点,求![]() 的值并证明:
的值并证明: ![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定集合A={a1 , a2 , a3 , …,an}(n∈N* , n≥3)中,定义ai+aj(1≤i<j≤n,i,j∈N*)中所有不同值的个数为集合A两元素和的容量,用L(A)表示.若数列{an}是公差不为0的等差数列,设集合A={a1 , a2 , a3 , …,a2016},则L(A)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在[﹣ ![]() ,
, ![]() ]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
]的函数f(x)=sinx(cosx+1)﹣ax,若y=f(x)仅有一个零点,则实数a的取值范围是( )
A.( ![]() ,2]
,2]
B.(﹣∞, ![]() )∪[2,+∞)
)∪[2,+∞)
C.[﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() ]∪(
]∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com