附加题:(本题共6分,附加题的得分直接加入总分,总分最高分不超过150分)
已知函数f(x)=lgsin(cosx)
(1)求y=f(x)的定义域;
(2)判断函数的奇偶性,并说明理由;
(3)求y=f(x)的单调区间.
【答案】
分析:(1)这里的cosx以它的值充当角,要使sin(cosx)>0转化成2kπ<cosx<2kπ+π,注意cosx自身的范围.
(2)根据奇偶性的定义进行判断;
(3)根据复合函数单调性的判断方法判断:设y=lgu,u=sint,t=cosx,
因为0<t≤1,所以y═lgu,u=sint都单调递增,所以y=f(x)的单调性与t=cosx单调性一致,由此即可判断.
解答:解:(1)由sin(cosx)>0⇒2kπ<cosx<2kπ+π(k∈Z).
又∵-1≤cosx≤1,
∴0<cosx≤1;
故所求定义域为{x|x∈(2kπ-
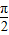
,2kπ+
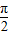
),k∈Z}.
(2)由(1)知y=f(x)的定义域为(2kπ-
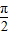
,2kπ+
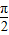
)(k∈Z),
关于原点对称,又f(-x)=f(x),
所以y=f(x)为偶函数.
(3)设y=lgu,u=sint,t=cosx,
因为0<t≤1,所以y═lgu,u=sint都单调递增,
故当2kπ-
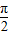
<x≤2kπ时,t=cosx单调递增,
所以y=f(x)的单调递增区间为(2kπ
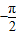
,2kπ](k∈Z),
当2kπ<x<2kπ+

时,t=cosx单调递减,
所以y=f(x)的单调递减区间为(2kπ,2kπ
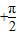
).
点评:本题主要考查了函数的定义域及其求法及复合函数单调性的判断,求三角函数的定义域,要解三角不等式,常用的方法有二:一是图象,二是三角函数线.

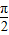 ,2kπ+
,2kπ+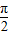 ),k∈Z}.
),k∈Z}.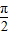 ,2kπ+
,2kπ+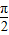 )(k∈Z),
)(k∈Z),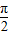 <x≤2kπ时,t=cosx单调递增,
<x≤2kπ时,t=cosx单调递增,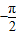 ,2kπ](k∈Z),
,2kπ](k∈Z), 时,t=cosx单调递减,
时,t=cosx单调递减,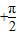 ).
).

 活力课时同步练习册系列答案
活力课时同步练习册系列答案