解:(I)∵f′(x)=cosx,f′(0)=1,
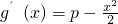
,g′(0)=p,
y=f(x)与y=g(x)在(0,0)处有相同的切线,
∴p=1…(3分)
(II)设F(x)=f(x)-g(x),
当p=1时,F(x)=sinx-x+
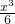
,
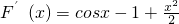
,
F''(x)=-sinx+x,
当x∈(0,1)时,sinx<x,故F''(x)>0,
从而F′(x)在(0,1)上单调增,
所以,F′(x)>F′(0)=0,
∴F(x)在(0,1)上单调增,
∴F(x)>f(0)=0,即f(x)>g(x)恒成立.
(III)当x∈(0,1)时,
∵F''(x)=-sinx+x>0,
∴F(x)在(0,1)上单调增,从而F(x)在(0,1)内不可能出现先增后减的情况,
∵F(0)=0,
∴要使F(x)>0在(0,1)上恒成立,
必有F(x)在(0,1)上单调递增,
即F′(x)≥0在x∈(0,1)上恒成立,
∵F′(x)
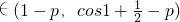
,
∴1-p≥0,
即p≤1.
分析:(I)由f′(x)=cosx,f′(0)=1,
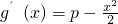
,g′(0)=p,知p=1.
(II)设F(x)=f(x)-g(x),当p=1时,F(x)=sinx-x+
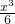
,
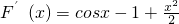
,F''(x)=-sinx+x,当x∈(0,1)时,F′(x)>F′(0)=0,由此能够证明(x)>g(x)恒成立.
(III)当x∈(0,1)时,由F''(x)=-sinx+x>0,知F(x)在(0,1)上单调增,从而F(x)在(0,1)内不可能出现先增后减的情况,由此能够求出p的范围.
点评:本题考查函数的恒成立问题,解题时要认真审题,仔细解答,注意导数的合理运用.

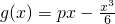
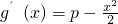 ,g′(0)=p,
,g′(0)=p,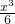 ,
,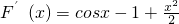 ,
,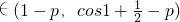 ,
,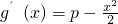 ,g′(0)=p,知p=1.
,g′(0)=p,知p=1.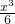 ,
,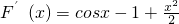 ,F''(x)=-sinx+x,当x∈(0,1)时,F′(x)>F′(0)=0,由此能够证明(x)>g(x)恒成立.
,F''(x)=-sinx+x,当x∈(0,1)时,F′(x)>F′(0)=0,由此能够证明(x)>g(x)恒成立.

 智慧小复习系列答案
智慧小复习系列答案